On this Page:
1. Definition of Zero\Root
2. Zeros on Graph
3. Zeros and Degree
4. Factor, Remainder Theorem
1. Definition of Zero\Root
2. Zeros on Graph
3. Zeros and Degree
4. Factor, Remainder Theorem
The factoring polynomials page introduced the concept of factors of polynomials.
Which is a topic that leads into understanding zeros of polynomials, also referred to as roots.
Definition of a Zero/Root
A value x = t is a zero/root of a polynomial p(x), if p(t) = 0.
So t is a zero/root, if it is a solution to p(x) = 0.
For example a polynomial we can look at is p(x) = x^2 + 5x + 6.
A root/zero will be an x value where x^2 + 5x + 6 = 0.
Looking at x = {\text{-}}2. p({\text{-}}2) = ({\text{-}}2)^2 + 5({\text{-}}2) + 6 = 0
So x = {\text{-}}2 is a zero/root.
It ‘s shown on the polynomial factors page how a polynomial,
p(x) = \space a_nx^n \space + \space a_{n \space {\text{–}} \space 1}x^{n \space {\text{–}} \space 1} \space + ….. + \space a_{\tt{2}}x^{\tt{2}} \space \space + a_1x \space + \space a_0
can be factored to p(x) = \space (x \space {\text{–}} \space t)(x \space {\text{–}} \space u)(x \space {\text{–}} \space v)…...
With the values of t, u, v ….
where (x \space {\text{–}} \space t) = 0 \space\space , \space\space (x \space\space {\text{–}} \space u) = 0 \space\space , \space\space (x \space {\text{–}} \space v) = 0 \space …..
being the roots\zeros of the polynomial.
So we’re looking for a polynomials factors in order to obtain the roots/zeros.
Zeros of Polynomials on a Graph:
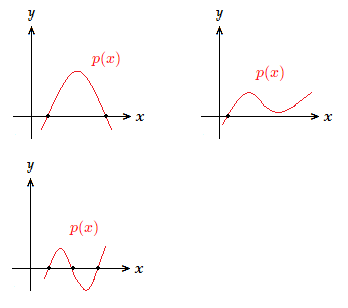
Polynomial Degree:
The number of factors a polynomial has being determined by the value of the ‘degree’ of the polynomial, means that the number of zeros/roots also is indicated by the degree, which is highest power/index of a variable that is present.4x + 5 is a polynomial of degree 1, and has one solution.
x^2 + 3x \space {\text{–}} \space 5 is a polynomial of degree 2 and has two solutions.
4x^3 + x^2 \space {\text{–}} \space 6x + 7 is a polynomial of degree 3, so having three solutions, and so on.
Examples
We can recap some quadratic polynomials where we have two factors and solutions.
(1.1)
x^2 \space {\text{–}} \space x \space {\text{–}} \space 6 = 0 => (x + 2)(x \space {\text{–}} \space 3) = 0
x = {\text{-}}2 \space , \space x = 3
(1.2)
x^2 + 2x + 1 = 0 => (x + 1)(x + 1) = 0
x = {\text{-}}1
Technically two solutions, they just happen to be the same.
Zeros of Polynomials,
Factor and Remainder Theorem
When it comes to establishing and finding zeros of polynomials that are larger than a quadratic and of degree 3 or larger.
The ‘factor theorem’ and the ‘remainder theorem’ can often be very helpful in assisting.
The wording can vary slightly from website to website when stating the theorems, but we’ll summarise here.
Factor Theorem:
For a polynomial f(x), when f(c) = 0.Then (x \space {\text{–}} \space c) is a factor of f(x).
Remainder Theorem:
When a polynomial f(x) is divided by (x \space {\text{–}} \space c).Then the remainder is f(c).
Examples
(2.1)
Determine if (x \space {\text{–}} \space 3) is a factor of f(x) = x^3 + 2x^2 \space {\text{–}} \space 11x \space {\text{–}} \space 12.
Solution
If (x \space {\text{–}} \space 3) is a factor, from the factor theorem we expect to see f(3) = 0.
f(3) = 3^3 + 2(3)^2 \space {\text{–}} \space 11(3) \space {\text{–}} \space 12 \space = \space 27 + 18 {\text{–}} \space 33 \space {\text{–}} \space 12 \space = \space 0
f(3) = 0, so (x \space {\text{–}} \space 3) is a factor of f(x).
Subsequently from the remainder theorem, x = 3 is a zero.
(2.2)
Which of -2, -1, 1 are zeros of f(x) = 2x^3 + 7x^2 + x \space {\text{–}} \space 10.
Solution
When a value c is a zero of f(x), then f(c) will be zero.
f({\text{-}}2) = 2({\text{-}}2)^3 + 7({\text{-}}2)^2 + {\text{-}}2 \space {\text{–}} \space 10 \space = \space {\text{-}}16 + 28 \space {\text{–}} \space 2 \space {\text{–}} \space 10 \space = \space 0
f({\text{-}}1) = 2({\text{-}}1)^3 + 7({\text{-}}1)^2 + {\text{-}}1 \space {\text{–}} \space 10 \space = \space {\text{-}}2 + 7 \space {\text{–}} \space 1 \space {\text{–}} \space 10 \space = \space {\text{-}}6
f(1) = 2(1)^3 + 7(1)^2 + 1 \space {\text{–}} \space 10 \space = \space 2 + 7 + 1 \space {\text{–}} \space 10 \space = \space 0
-2 and 1 are zeros of f(x) = 2x^3 + 7x^2 + x \space {\text{–}} \space 10.