Ratio and Proportion
A question that is often asked in more basic Statistics is what is proportion in Math?
When we have two ratios, they are classed as being in proportion if they are both equal to each other in measure.
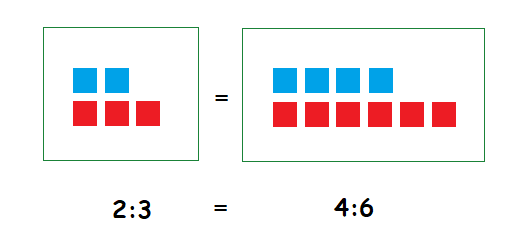
The ratios illustrated above, 2 : 3 and 4 : 6 are ratios that are in proportion.
“3 is to 4” as “4 is to 6”or
“3 out of 4” is the same ratios as “4 out of 6“.
Ratios can also be written as fractions too, so we can represent things this way.
\bf{\frac{2}{3}} = \bf{\frac{4}{6}}.
Notation for Proportion
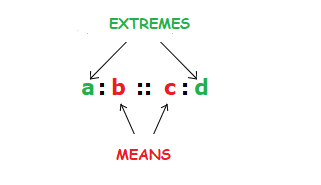
Say we have two different ratios that are in proportion, a:b = c:d.When this is the case we can write the ratios as, a:b :: c:d.
This means that a is to b, as c is to d.
The figures that are in the outer places, a and d, are referred to as “extremes”.
The figures in the inner places, b and c, are referred to as “means”.
What is Proportion in Math?
Looking for Proportion
In order to check if 2 ratios are in proportion, we can multiply the means, and the extremes together.
Because if 2 ratios form a proportion, then these multiplications will be equal in value.
Example
The ratios demonstrated earlier in the page were 2 : 3 and 4 : 6.
Multiplying the means and the extremes together gives:
3 × 4 = 12 , 2 × 6 = 12
2 : 3 and 4 : 6 do form a proportion.
2 : 3 :: 4 : 6
But what if we looked at the ratios.
3 : 4 and 5 : 7.
Multiplication of the means and the extremes together results in:
4 × 5 = 20 , 3 × 7 = 21
3 : 4 and 5 : 7 do NOT form a proportion.
We could also write the ratios in fraction form, and this approach is the same as comparing the cross products.
\bf{\frac{3}{4}} , \bf{\frac{6}{8}} => 3 × 8 = 24 4 × 6 = 24
\bf{\frac{3}{4}} , \bf{\frac{5}{7}} => 3 × 7 = 21 4 × 5 = 20
Proportion in Math Examples
(1.1)
If 3 : 7 and b : 14 form a proportion, what is the value of b?
Solution
For the two ratios to form a proportion, the ‘means’ and ‘extremes’ being multiplied together will produce an equal result.
3 × 14 = 7 × b => 42 = 7b
\boldsymbol{\frac{42}{7}} = b => b = 6
(1.2)
If \boldsymbol{\frac{6}{a}} and \bf{\frac{2}{19}} form a proportion, what is the value of a?
Solution
For the two ratios to form a proportion, the ‘means’ and ‘extremes’ again being multiplied together will produce an equal result.
6 × 19 = a × 2 => 114 = 2a
\boldsymbol{\frac{114}{2}} = a => a = 57
(1.3)
A lesser scale model is to created of a life size 4×4 car.
Based on the information seen in the image below, what height in cm should the smaller 4×4 model car be?
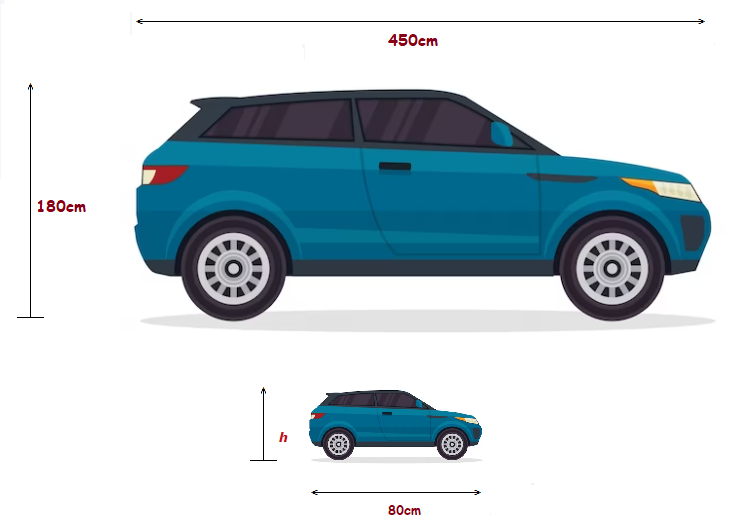
Solution
As the smaller size model is to be the same scale as the full size car, the width and height of each car will be in proportion with the other.
Thus we can solve for the height of the model car by drawing up the ratios of width to height.
\boldsymbol{\frac{WIDTH}{HEIGHT}} = \bf{\frac{450}{180}} = \boldsymbol{\frac{80}{h}}
450 × h = 180 × 80
450h = 14’400
h = \bf{\frac{14’400}{450}} = 32
The lesser scale 4×4 car model should be 32cm in height for the cars to be in proportion.
- Home ›
- Probability/Stats › Proportion