Simultaneous equations are equations that appear together at the same time. Like with standalone equations, they can often be solved for the relevant variables present.
Solving simultaneous equations is generally more complicated than solving a single equation by itself.
When we have simultaneous equations together we can call them a system of linear equations.
An example of which is:
2x + \space y = \space 3
3x \space {\text{--}} \space 7y = 10
A system of linear equations can have more than two equations present, sometimes many more, and more than two variables also.
But introductory examples for the topic often focus on simultaneous equation solving where there are two equations and two unknown variables.
Solving Simultaneous Equations Approach
Solving simultaneous equations involves finding the variable values that satisfy both equations together.
Take for example the following two simultaneous linear equations.
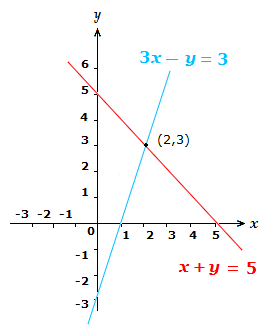
\space x + y = \space 5
3x \space {\text{--}} \space y = 3
There are probably many values for the variables x and y that will solve one of the equations on its own.
But only one set of values for the variables that will solve both equations at the same time.
The second solving simultaneous equations page shows how to actually solve for a system of two linear equations. However here below we will simply state the values of x and y that solve the equations together.
Solutions of Simultaneous Equations:
The values that solve both equations above are: x = 2 \space , \space y = 3.2 + 3 = 5
3(2) \space {\text{--}} \space 3 = 3
These values for the solutions serve a purpose of making up the coordinates of the point of intersection between the two lines of the equations if they were drawn graphically.
The diagram below shows the straight lines of both equations drawn graphically,
and the point of intersection is (2,3).
Simultaneous Equations,
No Solution
Simultaneous equations can sometimes have no solution for the variables that can be found.
For example,
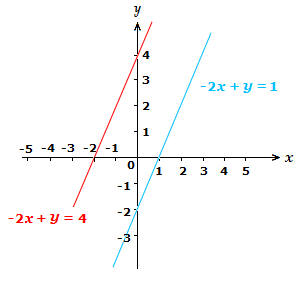
{\text{-}}2x + y = \space 4
{\text{-}}2x + y = {\text{-}}1
have no x and y values that solve both equations together.
Graphically this means that the straight lines for the equations will be parallel, and thus having the same slope as each other. As we can see in the diagram below.
More on how to solve simultaneous equations can be seen on the solving by substitution and elimination page.