The inequalities Introduction page introduced the concept of inequalities in Math, with a selection of examples involving numbers.
Along with also explaining how the different operations in Math can affect the nature of an inequality.
Solving linear inequalities examples when a variable or variables are present builds on that introduction, and in fact follows a similar logic to solving linear equations.
We again want to get a variable by itself on one side of the inequality symbol that is present, in the same way that we would with an equals sign in an equation.
Solving Linear Inequalities Approach:
A basic linear equation we could encounter is, x + 3 = 8.
To solve this equation, we can subtract 3 from both sides to get the variable x by itself, which provides a solution.
x + 3 \space {\text{--}} \space 3 \space = \space 8 \space {\text{--}} \space 3 , x = 5
This equation could also be written as a linear inequality, x + 3 \lt 8.
Which can also be solved in the same way.
However this time, instead of solving to find a value of x that added to 3 results in 8.
We are solving for the values of x which added to 3, gives a result less than 8.
x + 3 \space {\text{--}} \space 3 \space \lt 8 \space {\text{--}} \space 3 , x \lt 5
So the solution to the linear inequality is any x value less than 5.
Just like with equations, we can perform operations on inequalities to help us obtain solutions.
Solving Linear Inequalities Examples
(1.1)
Solve 2 + x \lt 5.
Solution
2 + x \space {\text{--}} \space 2 \space \lt \space 5 \space {\text{--}} \space 2
x \space \lt \space 3
x values less than 3 are solutions to the inequality.
(1.2)
Solve 3x \space {\text{--}} \space 1 \gt 14.
Solution
3x \space {\text{--}} \space 1 + 1 \space \gt \space 14 + 1
3x \gt 15
\frac{3x}{3} \space {\footnotesize{\gt}} \space \frac{15}{3}
x \gt 5
x values greater than 5 are solutions to the inequality.
(1.3)
Solve 6a \space \le \space 4a + 12.
Solution
6a \space {\text{--}} \space 4a \space \le \space 4a + 12 \space {\text{--}} \space 4a
2a \space \le \space 12
\frac{2a}{2} \space \le \space \frac{12}{2}
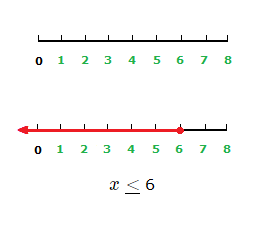
a \le 6
a values less than or equal to 6 are solutions to the inequality.
(1.4)
Solve 5(x + 4) \lt 30.
Solution
5x + 20 \lt 30
5x + 20 \space {\text{--}} \space 20 \space \lt \space 30 \space {\text{--}} \space 20
5x \space \lt \space 10
\frac{5x}{5} \space {\footnotesize{\lt}} \space \frac{10}{5}
x \le 2
x values less than 2 are solutions to the inequality.
Solving Linear Inequalities Examples,
Graphs
Sometimes when solving linear inequalities, we can be asked to sketch a graph of the linear inequality solution.
We can do this by drawing a relevant number line, and then on that number line sketch another line representing the values of the solution.
We can look at graphing the solutions to examples (1.2) and (1.3).
The solution to example (1.2) was x \gt 5.
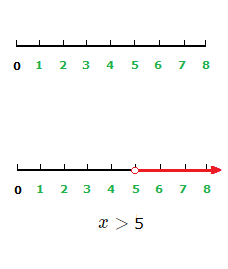
When the solution to the inequality doesn’t include the number found, there is an empty circle used in the graph.
The solution to example (1.3) was x \le 6.