The sets and set notation introduction page laid out the concept of sets in Math, and how to properly use set notation to represent sets.
Now this sets and Venn diagrams page will demonstrate how sets and set relationships can be presented as an illustration with what are called ‘Venn diagrams’, named after English mathematician John Venn.
Sets and Venn Diagrams,
Illustrating Sets with Venn Diagrams
We draw a circle or an ellipse to represent a set, more than one set will require more than one circle/ellipse to be drawn, and they can overlap depending on the specific elements within each set.
Added to that, a rectangle shape can be drawn around the circles to represent the Universal set, which contains every set and element that we are working with.
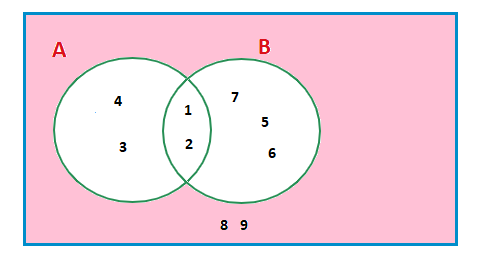
Consider 2 sets A and B, and the universal set U containing them.
A = { 1 , 2 , 3 , 4 } , B = { 1 , 2 , 5 , 6 , 7 }
U = { 1, 2 , 3 , 4, 5 , 6 , 7, 8 , 9 }
In a Venn diagram:
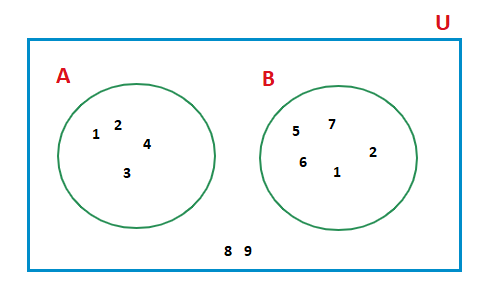
Now although the elements 8 and 9 are not in set A or set B.
They are still part of our Universal set here that contains both sets.
Now we will look at examples of sets and venn diagrams where we can shade parts of the diagram according the an appropriate set notation.
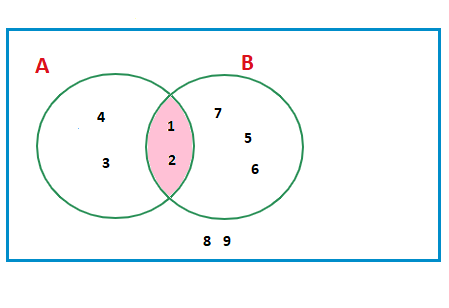
Sets Intersection A∩B
Notice that sets A and B share some elements, 1 and 2.
What this means is that we can redraw the Venn diagram with circles for sets A and B that overlap, so we can place the shared elements inside both of the sets together.
This overlapping section of the circles pictured below, which has been shaded, contains the elements inside both A and B .
In set notation this area is A∩B. The intersection of A and B.
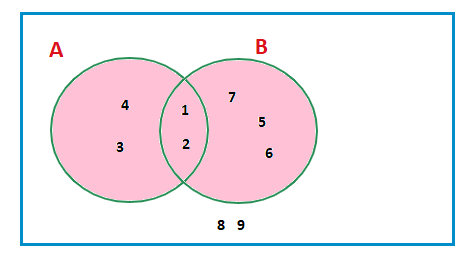
Sets Union A∪B
In the venn diagram we can also shade the areas with elements that are inside A or B.The union of A and B.
Elements in set A, not set B
The elements inside set A but NOT inside set B, A\B.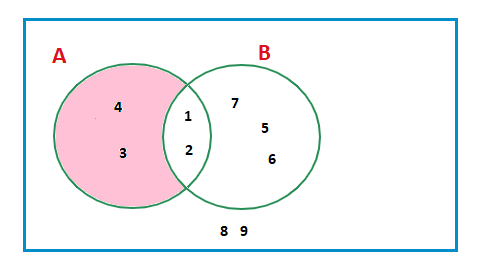
Set Compliment
With sets and venn diagrams we can also represent the situation where we focus on all the elements NOT in a set, the set compliment.
We can concentrate on the elements NOT in set A, Ac.
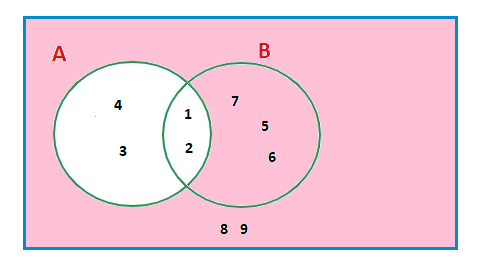
Elements not in set A and set B
We can shade the compliment of sets A and B together, ( A∩B )c.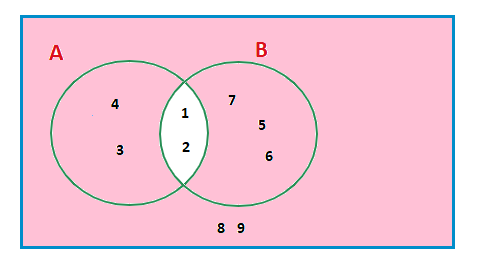
Elements not in set A or B
We can shade the compliment of sets A or B together, ( A∪B )c.