Trying to find roots of complex numbers can often be a bit trickier than working out powers.
Where you have to solve for the likes of:
z = (2 − 5i){\frac{1}{3}} or z = (3i){\frac{1}{4}}.
These examples can be re-written as:
z3 = (2 − 5i) and z4 = (3i).
How many solutions there are, depends on the value of the power/exponent.
z3 = (2 − 5i) , 3 solutions/roots to find.
z2 = (2 − 5i) , 2 solutions/roots to find.
So for zn = (2 − 5i) , there would be n solutions/roots to find.
How to Approach Solving
For a complex number in Cartesian form like the one above, we can convert to Polar form.When we have a number like z = 2 − 5i in its Polar form, zn = r(cosθ + isinθ).
In order to find the nth roots, the following formula can be used:
n√z = n√r (cos( {\frac{\theta}{n}} + {\frac{2 \pi k}{n}} ) + isin( {\frac{\theta}{n}} + {\frac{2 \pi k}{n}} )
Solving for k = 0,1,2,…..,n − 1.
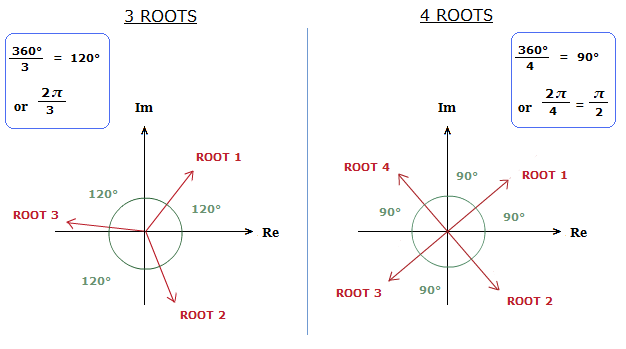
The roots/solutions found will also be complex numbers, that can be drawn as vectors on the Argand Diagram.
The vectors will be the same size, be evenly spread out, and the angle between them will depend on how many vectors there are.
Find Roots of Complex Numbers Example
(1.1)
Find the roots of z = (1 + √3i){\frac{1}{3}}
Solution
We can be rewrite slightly as z3 = (1 + √3i).
Now putting z3 into polar form:
θ = tan-1(\bf{\frac{\sqrt{3}}{1}}) = \bf{\frac{\pi}{3}} , r = \bf{\sqrt{1^2 \space + \space(\sqrt{3})^2}} = 2
=> z3 = 2(cos(\bf{\frac{\pi}{3}}) + isin(\bf{\frac{\pi}{3}})
Then applying the formula:
\bf{^3\sqrt{z}} = \bf{^3\sqrt{2}} (cos( {\frac{\pi/3}{3}} + {\frac{2 \pi k}{3}} ) + isin( {\frac{\pi/3}{3}} + {\frac{2 \pi k}{3}} ))
\bf{^3\sqrt{z}} = \bf{^3\sqrt{2}} (cos( \bf{\frac{\pi}{9}} + {\frac{2 \pi k}{3}} ) + isin( \bf{\frac{\pi}{9}} + {\frac{2 \pi k}{3}} ))
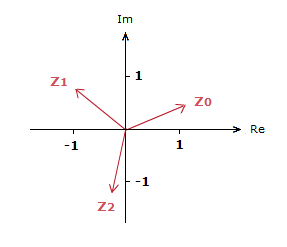
The 3 solutions/roots to find are when the values of k = 0,1,2.
k = 0:
z0 = \bf{^3\sqrt{2}} (cos( \bf{\frac{\pi}{9}} ) + isin( \bf{\frac{\pi}{9}} ))
= 1.18 + i0.43
k = 1:
z1 = \bf{^3\sqrt{2}} (cos( \bf{\frac{\pi}{9}} + \bf{\frac{2\pi}{3}} ) + isin( \bf{\frac{\pi}{9}} + \bf{\frac{2\pi}{3}} ))
= \bf{^3\sqrt{2}} (cos( \bf{\frac{7\pi}{9}} ) + isin( \bf{\frac{7\pi}{9}} ))
= –0.97 + i0.81
k = 2:
z2 = \bf{^3\sqrt{2}} (cos( \bf{\frac{\pi}{9}} + \bf{\frac{4\pi}{3}} ) + isin( \bf{\frac{\pi}{9}} + \bf{\frac{4\pi}{3}} ))
= \bf{^3\sqrt{2}} (cos( \bf{\frac{13\pi}{9}} ) + isin( \bf{\frac{13\pi}{9}} ))
= –0.22 − i1.24
On the Argand Diagram.
There can be slightly differing methods to compute the roots of complex numbers depending on the situation.
But the approach above is an effective way to tackle these types of questions.
A slightly different approach for finding the values of complex number roots can be seen here.
Along with some good in depth information on the theory behind the roots of complex numbers.