Complex numbers can be solutions to equations in Math at times.
This page will focus on quadratic equations with complex solutions as an introduction to the topic.
Let’s consider 2 standard quadratics and look at their respective graphs.
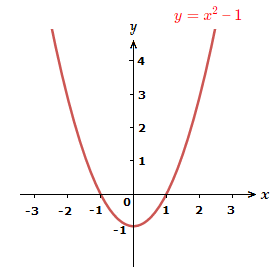
It can be seen that the graph of y = x^2 \space {\text{--}} \space 1 does touch the x-axis and has roots at 2 points.
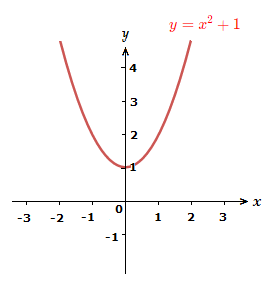
Where as the graph of y = x^2 + 1 does not touch the x-axis at any point, it has no real roots.
Solving the Quadratics as Equations
We can write these quadratics as equations equal to 0.
Then solve and find any roots.
– x^2 \space {\text{--}} \space 1 = 0 => x^2 = 1 => \sqrt{x^2} = \pm \sqrt{1} => x = \pm 1
– x^2 + 1 = 0 => x^2 = {\text{-}}1 => \sqrt{x^2} = \pm \sqrt{{\text{-}}1} => x = \pm i
As expected for x^2 \space {\text{--}} \space 1 = 0, we get the real solutions of -1 and 1.
But for x^2 + 1 = 0, even though there are no real solutions, we do get two complex solutions of –i and i.
NOTE:
Finding two complex solutions together is actually a general case for quadratic equations with complex solutions.
They occur in ‘conjugate pairs’, one with a positive sign and one with a negative sign, which we will see in examples further on in the page.
Making use of the Discriminant:
If we recall the discriminant of a quadratic, this is a value that tells us what the nature of roots of a quadratic equation will be.The formula for the discriminant is the portion inside the radical of the quadratic formula.
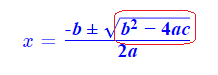
So to recap, for a quadratic equation ax^2 + bx + c = 0.
The value of the discriminant tells us.
\boldsymbol{{b^{2}} - 4ac} > 0 There are two different real roots.
\boldsymbol{{b^{2}} - 4ac} = 0 There are two equal real roots, so one root in total.
\boldsymbol{{b^{2}} - 4ac} < 0 There are no real roots, instead there are two complex solutions.
So the working discriminant is a handy way of finding out in advance what kind of roots/solutions you can expect to see for a quadratic equation.
Quadratic Equations with Complex Solutions
Examples
(1.1)
Find the roots of x^2 \space {\text{--}} \space 3x + 9 = 0.
Solution
a = 1 \space\space , \space\space b = {\text{-}}3 \space\space , \space\space c = 9
We can solve using the quadratic formula.
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}b \space \pm \space \sqrt{b^{2} \space - \space 4ac}}{2a}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{3 \space \pm \space \sqrt{({\text{-}}3^{2} \space\space - \space\space (4 \times 1 \times 9)}}{2 \times 1}}} = {\boldsymbol{\frac{3 \space \pm \space \sqrt{9 \space\space {\text{--}} \space\space 36}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{3 \space \pm \space \sqrt{{\text{-}}25}}{2}}} = {\boldsymbol{\frac{3 \space \pm \space \sqrt{25 \space \times \space {\text{-}}1}}{2}}} = {\boldsymbol{\frac{3 \space \pm \space \sqrt{25}\sqrt{{\text{-}}1}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{3 \space \pm \space 5i}{2}}}
Which we can alternatively write as {\boldsymbol{\frac{3}{2} {\scriptsize{\pm}} \frac{5i}{2}}}.
(1.2)
Find the roots of x^2 \space {\text{--}} \space x + 2 = 0.
Solution
a = 1 \space\space , \space\space b = {\text{-}}1 \space\space , \space\space c = 2
{\scriptsize{x = \space}} {\boldsymbol{\frac{1 \space \pm \space \sqrt{({\text{-}}1^{2} \space\space - \space\space (4 \times 1 \times 2)}}{2 \times 1}}} = {\boldsymbol{\frac{1 \space \pm \space \sqrt{1 \space\space {\text{--}} \space\space 8}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{1 \space \pm \space \sqrt{{\text{-}}7}}{2}}} = {\boldsymbol{\frac{1 \space \pm \space \sqrt{7 \space \times \space {\text{-}}1}}{2}}} = {\boldsymbol{\frac{1 \space \pm \space \sqrt{7}\sqrt{{\text{-}}1}}{2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{1 \space \pm \space \sqrt{7}i}{2}}} or {\boldsymbol{\frac{1}{2} {\scriptsize{\pm}} \frac{\sqrt{7}i}{2}}}
(1.3)
Find the roots of {\text{-}}x^2 + 4x \space {\text{--}} \space 6 = 0.
Solution
a = {\text{-}}1 \space\space , \space\space b = 4 \space\space , \space\space c = {\text{-}}6
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{({\text{-}}4)^{2} \space\space - \space\space (4 \times ({\text{-}}1) \times ({\text{-}}6))}}{2 \space \times \space ({\text{-}}1)}}} = {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{16 \space\space {\text{--}} \space\space 24}}{{\text{-}}2}}}
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{{\text{-}}8}}{{\text{-}}2}}} = {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{8 \space \times \space {\text{-}}1}}{{\text{-}}2}}} = {\boldsymbol{\frac{{\text{-}}4 \space \pm \space \sqrt{8}\sqrt{{\text{-}}1}}{{\text{-}}2}}}
( \bf{\sqrt{8}} can be simplified further to \bf{2\sqrt{2}}. )
{\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}4 \space \pm \space 2\sqrt{2}i}{{\text{-}}2}}} = {\boldsymbol{\frac{{\text{-}}4}{{\text{-}}2} \space {\scriptsize{\pm}} \space \frac{2\sqrt{2}i}{{\text{-}}2}}}
x = \space {\boldsymbol{2 \space \pm \sqrt{2}i}}