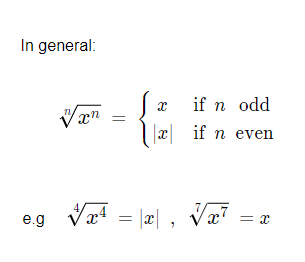On this Page:
1. Radical and Exponent Form
2. Radical Properties
3. Simplifying Radical Form Examples
1. Radical and Exponent Form
2. Radical Properties
3. Simplifying Radical Form Examples
In Algebra, we often have to simply terms with radicals involving number or variables, or sometimes both.
There are some properties of radicals that are handy to remember as they can help with simplifying when required.
Radical and Exponent Form:
If we recall a basic radical definition from the fraction exponents page, and how radicals can be written in exponent form.{\large{\sqrt[n]{a}}} \space = \space {\large{a}}^{\frac{1}{n}}
{\large{\sqrt[n]{a}}} is the ‘radical’ form , {\large{a}}^{\frac{1}{n}} is the ‘exponent’ form.
Examples
(1.1)
{\large{\sqrt[6]{2x}}} is ({\large{2x}})^{\frac{1}{6}} in exponent form.
(1.2)
{\large{2\sqrt[6]{x}}} is {\large{2x}}^{\frac{1}{6}} in exponent form.
(1.3)
\sqrt{x + y^3} is ({x + y^3})^{\frac{1}{2}} in exponent form.
Properties of Radicals, Simplifying
The following properties of radicals apply when m and n are integers,
and x, \space y are real numbers greater than zero.
1) {\large{\sqrt[n]{x^n}}} \space = \space {\large{x}} 2) {\large{\sqrt[n]{x^m}}} \space = \space {\large{x}}^{\frac{m}{n}}
3) {\large{\sqrt[n]{xy}}} \space = \space {\large{\sqrt[n]{x}\sqrt[n]{y}}}
4) {\frac{\sqrt[n]{x}}{\sqrt[n]{y}}} \space = \space \sqrt[n]{\frac{x}{y}}
Simplifying Radical Form:
Knowing the above properties can help when it’s required to simplify an expression in Math that involves a one or more radical terms.When we want to simplify a radical we have several main aims to achieve.
– Any exponents inside the radical should not be greater than the radical index.
– Have no fractions inside the radical.
– Have no radicals as the denominator in a fraction.
– An exponent in the radicand will not share a factor with the index of the radical.
Examples
(2.1)
Simplify \sqrt{x^3}.
Solution
Remembering that \sqrt{x^3} is \sqrt[2]{x^3} in full notation.
We will want to make sure that the radicand inside the radical doesn’t have a term with an exponent greater than 2.
\sqrt{x^3} \space = \space \sqrt{x^{2}x} \space = \space \sqrt{x^2}\sqrt{x} \space = \space x\sqrt{x}
(2.2)
Simplify \sqrt{x^{5}y^{2}}.
Solution
\sqrt{x^{5}y^{2}} \space = \space \sqrt{x x^{2} x^{2} y^{2}} \space = \space \sqrt{x}\sqrt{x^2}\sqrt{x^2}\sqrt{y^2} \space = \space \sqrt{x} x^2 y
(2.3)
Simplify \sqrt{18a^{16}bc^{13}}.
Solution
With a radical expression such as this one where there are index in the radicand that are larger numbers.
Property 2) listed above can be helpful to remember and make use of. {\large{\sqrt[n]{x^m}}} \space = \space {\large{x}}^{\frac{m}{n}}
\sqrt{18a^{16}bc^{13}} \space = \space \sqrt{9 \times a^{16}c^{12} \times 2 \times b \times c} \space = \space \sqrt{9}\sqrt{a^{16}}\sqrt{c^{12}}\sqrt{2bc}
= \space 3a^{16/2}c^{12/2}\sqrt{2bc} \space = \space 3a^8c^6\sqrt{2bc}
(2.4)
Simplify \frac{\sqrt{72}}{\sqrt{8}}.
Solution
Property 4) can be used to simplify cases like this one.
\frac{\sqrt{72}}{\sqrt{8}} \space = \space \sqrt{\frac{72}{8}} = \space \sqrt{9} \space = \space 3
Simplifying Radicals, Special Case:
In the properties list above we listed property 1) as, {\large{\sqrt[n]{x^n}}} \space = \space {\large{x}}.This is true, but it needs to be expanded on slightly for certain cases.
When x is negative and n is even.
If we look at an example of –3.
(-3)2 = (-3) × (-3) = 9
(-3)3 = (-3) × (-3) × (-3) = -27
So \sqrt[3]{({\text{-}}3)^3} \space = \space {\text{-}}3,
but \sqrt{({\text{-}}3)^2} \space = \space 3.
Therefore when n is even and we have a negative x, we take the absolute value of x, |x|.
As this makes the value positive.