1. Fractions in a Pie
2. Equivalent Fractions
3. Common Denominators
4. Proper and Improper Fractions
5. Mixed Fraction
When understanding fractions and learning how to write fractions, a good way to initially think of a fraction in its standard form, is as a part or parts of a greater whole.
This can be shown visually by looking at a simple shape and cutting it into parts.
Fractions in a Pie
We can look at a pie which is in the shape of a circle.
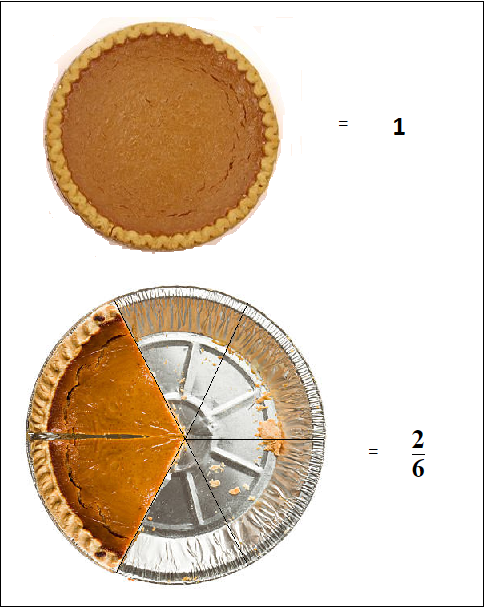
We started out with 1 whole pie.
This pie was then cut into 6 parts, and we were left with 2 of them remaining.
So we had 2 out of 6 parts of the pie. \bf{\frac{2}{6}}
How to Write Fractions,
Numerator and Denominator
For a clear explanation of how to write fractions.
With a standard fraction, the number on the top line is called the “NUMERATOR“,
and the number on the bottom line is called the “DENOMINATOR“.
A situation to also note is that when a fraction NUMERATOR and DENOMINATOR are the same value.
When this happens, the whole fraction value is the number 1.
1 = \bf{\frac{3}{3}} , 1 = \bf{\frac{7}{7}} and so on.
Equivalent Fractions
Equivalent Fractions are fractions that have different numerators and denominators, but turn out to actually have the same overall value.
As it turns out, equivalent fractions can also be referred to as equal fractions.
\bf{\frac{1}{3}} = \bf{\frac{2}{6}} = \bf{\frac{3}{9}}
These fractions share the same value, even though they have different numerators and denominators. They are equivalent or equal to each other.
Simplest Form of a Fraction:
Even though the above fractions were the same value/size,
it’s the case that \bf{\frac{1}{3}} is what is called the “simplest form”.
This is because the numerator and denominator of the fraction are both the smallest whole numbers that could be used in the fraction.
Common Denominators
When it’s the case that 2 or more fractions happen to have the same denominator as one another, then between them they have what is referred to as a “common denominator”.
The fractions: \bf{\frac{1}{6}} , \bf{\frac{2}{6}} , \bf{\frac{4}{6}}have the common denominator of 6.
While the fractions: \bf{\frac{2}{11}} , \bf{\frac{5}{11}} , \bf{\frac{10}{11}}
have a common denominator of 11.
Proper and Improper Fractions
It’s fairly straight forward to understand the difference between proper and improper fractions.
When the value of a fraction is less than 1, for example \bf{\frac{3}{4}},
the fraction is a “proper” fraction.
However a fraction can also have an overall value that is greater than or equal to 1.
Where the numerator on the top line is greater than or equal to the denominator on the bottom line. When this is the case, the fraction is then an “improper” fraction.
The fraction \bf{\frac{7}{4}} is a simple example of an improper fraction.
Improper fractions can sometimes be referred to as “top heavy fractions”. Because the numerator on top would be the greater number in the fraction.
Unit Fractions:
If you ever come across the term “unit fraction” when learning more about understanding fractions, this is just a fraction which has the numerator of 1 on the top line.
The fractions \bf{\frac{1}{4}} , \bf{\frac{1}{13}} , \bf{\frac{1}{762}} can be referred to as “unit fractions”.Mixed Fraction
A fraction can also be written as a “mixed fraction”, where there is a whole number part, along with a fraction part also.
Mixed fractions can at times also be referred to as mixed numbers.
An example of a mixed fraction is 3\bf{\frac{1}{6}}.
The whole number part is 3, while the fraction part of the number is \bf{\frac{1}{6}}.
To get an idea of this visually, we can again use a pie to illustrate.

We have 3 whole pies, and also \bf{\frac{1}{6}} of another pie.
- Home ›
- Fractions & Decimals › Understanding Fractions