Probability is a measure of how likely an event or outcome is to possibly occur.
Values of Probability
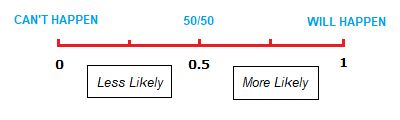
The value that a probability can have is a number between 0 and 1.
With probabilities with a value nearer to 0 being less likely to happen,
and probabilities with a value nearer to 1 being more likely to happen.
So an event having a probability of 0 means it can’t occur at all.
Where as an outcome having a probability of 1 means that it will definitely occur.
It’s handy to demonstrate this using a what we can call a “probability number line”, shown below.
Number Line for Probability:
How to Work out Probability
The Probability of a certain event can be established as a fraction sum.
Event Probability = \frac{\tt{\color{blue}Number \space of \space ways \space an \space event \space can \space happen}}{\tt{\color{red}Number \space of \space different \space possible \space outcomes}}The amount that is the number of different possible outcomes, is referred to as as the “SAMPLE SPACE“.
So the sample space in probability is the set of all the outcomes that are possible with a certain event.
Working out Probability Examples
Coin and Dice
Probability of Flipping a Coin

A good way to get introduced to probability is looking at the probability of flipping a coin.
We can write the probability of this event as a fraction sum.
The possible outcomes from flipping the coin, are a “HEAD” or a “TAILS”.
SAMPLE SPACE = { HEAD , TAILS }Let’s look at the probability of landing a head.
There is only 1 way that this event can happen,
and there are 2 possible outcomes from flipping a coin, we can land a HEAD or a TAILS.
Probability of a HEAD = \frac{\tt{\color{blue}Number \space of \space ways \space an \space event \space can \space happen}}{\tt{\color{red}Number \space of \space different \space possible \space outcomes}}
Probability of a HEAD = \bf{\frac{1}{2}}
It should be mentioned that it is also the case that probabilities can be written in the form of decimals.
The probability of landing a HEAD was \bf{\frac{1}{2}}.
Which is a fraction that can be written as 0.5.
Thus as a percentage, there is a 50% probability of landing a HEAD with the flip of a fair coin.
What about the probability of landing a HEAD or a TAILS?
In this case there are 2 possible ways that this can occur, and 2 possible outcomes in total.
Probability of a HEAD or a TAIL = \bf{\frac{2}{2}} = 1A probability value of 1 means that the result from a coin flip will definitely be either a HEAD or a TAILS.
Percentage wise a 100% probability.
Probability of Rolling a Dice

An example that expands further on the probability of flipping a coin, is the event of rolling a six standard sided dice, which is another good example to introduce probability in Math.
The sides of a standard dice are comprised of 6 different numbers.
Each of these numbers has the same probability of being rolled, \bf{\frac{1}{6}}.
Probability of Rolling an Odd Number:
There are 3 sides of the dice with an odd number, 1 , 3 , 5.
Probability of rolling an odd number = \bf{\frac{3}{6}} = \bf{\frac{1}{2}} = 0.5 = 50%
Probability of Rolling a 4:
There is just one side of the dice with a number 4.
Probability of rolling a 4 = \bf{\frac{1}{6}} = 0.1666 = 16.66%
Probability of Rolling a 9:
Now to think about the probability of rolling a number 9.
There turns out to be no side with the number 9 on a standard six sided dice.
So there are zero ways that this outcome can occur, however there are still six possible outcomes that could occur from rolling the dice.
Probability of rolling a 9 = \bf{\frac{0}{6}} = 0
A probability of 0 for rolling a 9, tells us that it can’t happen in any way.
There is a 0% probability.
Probability Notation
Probability notation is generally written with a capital “P“, accompanied by the relevant event that could occur.
P( Event ) =With the probability of flipping a coin example above, the probability of landing a HEAD was
Using appropriate notation for probability this would be written as:
P( HEAD ) = 50%
When dealing with the probability more then one event, there is symbols we use for “and” or “or” situations.
The probability of events A and B is notated.
P( A ∩ B )
The probability of events A or B is notated.
P( A ∪ B )
Probability Complement
The “probability complement”, is the probability of an event not happening.
With the rolling of a dice example above, we looked a the probability of rolling a number 4.
The probability compliment of that event is the probability of NOT rolling a number 4.
The notation for the complement can be done in one of several different ways.
Let’s say we have an event labelled simply as X, then the complement of this event can be written as:
Xc , X‘ or X.
The notation Ac is probably the form that will be encountered the most for the probability complement.
Probability of the Complement:
One important thing to realize and remember is that the probability of an event happening, and the probability of the event compliment, add up to 1.
P(X) + P(Xc) = 1As a consequence we get how to compute the value of the complement. P(Xc) = 1 − P(X)
So for the example with the rolling a dice earlier.
P( 5 ) = \bf{\frac{1}{6}}
Thus the complement which is NOT rolling a 5 can be worked out with the sum:
P( 5c ) = 1 − P(5) = 1 − \bf{\frac{1}{6}} = \bf{\frac{5}{6}}
Sample Space:
The sample space which represents all the possible outcomes of an event, is denoted with a capital “S“.So the sample space for rolling dice would be written as, S = { 1 , 2 , 3 , 4 , 5 , 6 }.
- Home ›
- Probability and Statistics › Probability Intro