There are a few effective ways to approach dividing polynomials. One approach is to use what is known as the polynomial division box method.
The box method can sometimes seem a bit tricky to get the hang of initially.
But once fully understood, it is an approach to polynomial division that can be very useful for a range of division sums.
Dividing Polynomials Recap:
The division of algebraic expressions page showed some basic examples of dividing some short polynomials.
Examples of polynomial division sums such as \frac{6x^{\tiny{4}} + 8x^{\tiny{2}}}{3x}.
\frac{6x^{\tiny{4}} + 8x^{\tiny{2}}}{3x} = \frac{6x^{\tiny{4}}}{3x} {\scriptsize{+}} \frac{8x^{\tiny{2}}}{3x} = {\scriptsize{2x^{\tiny{3}}} +} \frac{8x}{3}
But performing division when larger polynomials are involved often requires a bit more work, this is where an approach like the box method can come in handy.
Polynomial Division Box Method
Approach
We will introduce the box method by looking at the following division sum.
( 3x^{\tt{2}} + 2x \space {\text{–}} \space 1 ) \div ( x + 1 )
1)  Draw a standard box, and write the terms in the divisor on the left side from top to bottom.
Now split this larger box into some smaller boxes from left to right, from the divisor terms.
The divisor terms can be outside the larger box on the left side, or they can be in their own little boxes, as we have here, shown in lighter blue.
We’ve started with 3 extra boxes, but it may turn out that we don’t need to use all of them in obtaining the final answer.
| x | |||
| 1 |
( We want to reach a stage where with the entries in the white boxes, if we sum up the diagonals from lower left to top right, we get our original dividend. )
2) Write the first term in the dividend in the top left box beside the top divisor term.
Then divide this dividend term in the top left by the first divisor term, and place the result on top of the box above the column.
So here it’s the result of \frac{3x^{\tiny{2}}}{x}, which is 3x
| x   | 3x^{\tiny{2}} | ||
| 1 |
| x | 3x^{\tiny{2}} | ||
| 1 |
3) Multiply this new term on top by the next term of the divisor on the left side, and place the result in the box beside.
The result of 3x \times 1, 3x.
| x   |   3x^{\tiny{2}}   |         |         |
| 1   |   3x   |
4)  For the next entry in the next box, we look back at our original full dividend.   3x^{\tiny{2}} + 2x \space {\text{–}} \space 1
Diagonally up from left to right, what added to  3x,  will give us the  2x  in the dividend.
This will be  {\text{-}}x,  as  3x \space {\text{–}} \space x = 2x.
| x   |   3x^{\tiny{2}}   |   {\text{-}}x   |         |
| 1   |   3x   |
5)  Like before, we again divide this term by the first divisor term on the left, and place above.   \frac{{\text{-}}x}{x} = {\text{-}}1
| x   |   3x^{\tiny{2}}   |   {\text{-}}x   |         |
| 1   |   3x   |
We then like before multiply this new term above by the next term in the divisor on the left, then place in the next box below.   1 \times {\text{-}}1 = {\text{-}}1
| x   |   3x^{\tiny{2}}   |   {\text{-}}x   |         |
| 1   |   3x   |   {\text{-}}1   |
Now if we sum up the diagonals in the white boxes, we have our original dividend.
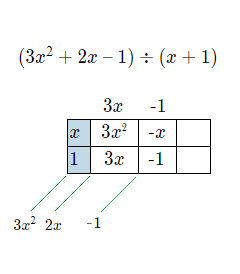
We now are complete with the box method for this polynomial division sum,
and the answer is the expression on top of the box.   3x \space {\text{–}} \space 1
( 3x^{\tt{2}} + 2x \space {\text{–}} \space 1 ) \div ( x + 1 ) \space = \space 3x \space {\text{–}} \space 1
Polynomial Division Box Method
with Remainder
It’s also important to know how to accommodate having a remainder with box method division.
We will look at a polynomial division sum that does have a remainder.
( 4x^{\tt{2}} + 3x + 2 ) \div ( x \space {\text{–}} \space 2 )
We will procced as usual until the first four white boxes are all filled in with terms.
1)
| x   | 4x^{\tiny{2}} |         |         |
| {\text{-}}2 |
2)
| x   | 4x^{\tiny{2}} |         |         |
| {\text{-}}2 |
3)
| x   | 4x^{\tiny{2}} |         |         |
| {\text{-}}2 | {\text{-}}8x |
4)
| x   | 4x^{\tiny{2}} | 11x |         |
| {\text{-}}2 | {\text{-}}8x |
5)
| x   | 4x^{\tiny{2}} | 11x |         |
| {\text{-}}2 | {\text{-}}8x |
6)
| x   | 4x^{\tiny{2}} | 11x |         |
| {\text{-}}2 | {\text{-}}8x | {\text{-}}22 |
Now we’ve reached the non x terms, we’re almost finished but not quite.
However unlike before, our fourth term in the white boxes isn’t the last term in the divided of   4x^{\tt{2}} + 3x + 2.
The final term is  2,  but we have  -22.
As we sum up our diagonal entries, we need to add something to  -22  that gives us  2,  this is  24.
7)
| x   |  4x^{\tiny{2}}  |  11x  |  24  |
| {\text{-}}2 | {\text{-}}8x | {\text{-}}22 |
Now we have our diagonal entries that sum up to give us the original dividend of   4x^{\tt{2}} + 3x + 2.
The answer to the polynomial division sum is the top expression of  4x + 11,  but we have the extra  24  to accommodate.
This  24  is the remainder, and it gets added on to  4x + 11  as a fraction over the divisor of the original sum.
So for the final answer to the sum we get,
  ( 4x^{\tt{2}} + 3x + 2 ) \div ( x \space {\text{–}} \space 2 ) \space\space = \space\space 4x + 11 + {\large{\frac{24}{x \space {\text{–}} \space 2}}}.