1. Effect of an Exponent
2. Exponents & Negative Numbers
3. Exponents & Roots
4. Surds
Exponents in the most basic form, tell us you how many times to perform multiplication of a number with itself.
An exponent can also be referred to as a power or an index.
When they appear, exponents are positioned at the top right of a base number.
The base number is the number that is to be multiplied with itself a set amount of times.
Sometimes more care needs to be taken when dealing with negative numbers and exponents,
as opposed to positive numbers.
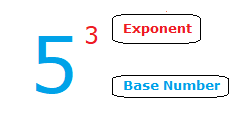
Effect of an Exponent
Exponents and roots are connected as we will see further on in this page, but to focus solely on exponents just now.
The value of the exponent is how many times we multiply the base number.
43 = 4 × 4 × 4 = 64 The number 4 multiplied with itself 3 times.
In general:
an = a × a × a × …….. × a n times. With n > 0
Negative Numbers and Exponents
Sometimes extra care needs to be taken when the base number is a negative number.
Consider two cases: ( –4 )2 and 42.
Both sums may appear to be the same, but there will be a difference in the result of each.
We need to remember that it is only the value directly on the left of the exponent that is affected by it.
The presence of brackets/parenthesis are what make the two above sums different.
1st Case
( –4 )2 = ( –4 ) × ( –4 ) = 16The brackets are directly on the left of the exponent, so everything that is in the brackets is affected by the exponent.
2nd Case
–42 = –(4 × 4) = –16Just the number 4 is the on the left of the exponent without the brackets, so it’s only the 4 that is affected.
The exponent was not on the minus sign, it was just connected to the number 4.
So as can be seen, it’s important to pay attention to the position of any brackets in a sum/expression involving an exponent.
As the same rules apply with variables and exponents as well as numbers.
Exponents and Roots
The connection between exponents and roots is that a root is a number that gives another number when raised to an appropriate exponent.
The symbol for representing roots of a number is the radical symbol \bf{\sqrt{\space \space}}.
Let’s look at the number 27.
This is written \bf{\sqrt[3]{27}}.
The small 3 in the upper left represents that this is the third root of 27.
So, \bf{{\sqrt[3]{27}} = 3}.
Square Roots and Cube Roots
The most common roots that most people are likely to encounter are square roots and cube roots.
Square roots are the second root of a number, \bf{\sqrt[2]{\space \space}}.
But generally we don’t write the number 2 in the upper left with square roots, so we just write as \bf{\sqrt{\space \space}}.
Thus the square root of 64 is written as, \bf{\sqrt{64}} = 8. ( As 8 × 8 = 64. )
Cube roots are the third root of a number.
For these roots and higher, the number is included in the upper left.
So the symbol for the cube roots is \bf{\sqrt[3]{\space \space}}.
The cube root of 64 is written as, \bf{\sqrt[3]{64}} = 4. ( As 4 × 4 × 4 = 64. )
Surds
When a root can’t be simplified to a whole number, it is an irrational number and is referred to as a “surd”.
\sqrt{10} is a surd.
As no matter how we rewrite or simplify, we can’t write it as a whole number.
\sqrt{9} is NOT a surd, as it can be simplified to a whole number.
\sqrt{9} = 3
For further reading on the topic of exponents, roots and radicals. The Algebra 1 section has more pages that go into further detail, and include examples covering the laws of exponents.