Dealing with multiplying polynomials examples isn’t really much more difficult than dealing with addition or subtraction of polynomials examples.
But care can often need to be taken with each step of multiplication performed.
FOIL Multiplication Method Recap:
When two polynomials being multiplied together are binomials, meaning they contain only two terms.The FOIL method of multiplication is an effective way to deal with such situations.
The FOIL method page showed how the process works, but we will show a quick recap here.
If we have, ( x + 2 ) \times ( x \space {\text{--}} \space 3).
FOIL means that we multiply in order.
Both ‘First’ terms, both ‘Outer’ terms, both ‘Inner’ terms, then both ‘Last’ terms, and add them all together.
So we have.
( x + 2 ) \times ( x \space {\text{--}} \space 3) \space = \space ( x \times x ) + ( x \times {\text{-}}3 ) + ( 2 \times x ) + ( 2 \times 3 )
= x^2 \space {\text{--}} \space 3x + 2x + 6 \space = \space x^2 \space {\text{--}} \space x + 6
However when we have larger polynomial multiplication sums to deal with, it’s often better to use an approach called vertical multiplication.
Polynomial Vertical Multiplication
In solving multiplying polynomials examples we can at times look to do vertical multiplication, where we place the polynomials on top of each other, usually best to start with the larger polynomial on top.We structure the sum so that the terms are in relevant columns with their other like terms, eg an x term with another x term.
Then we multiply each term in each polynomial with each term in the other polynomial.
Placing the results below, then adding them.
This is really best understood in observing an example.
We can look at multiplying ( x^{\tt{2}} + 3x \space {\text{--}} \space2 ) \times ( x + 2 ).
1) We start by laying the polynomials out as a vertical multiplication sum.
\begin{array}{r} \space x^{\tt{2}} + 3x \space {\text{--}} \space\space 2\\ \times \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space x + 2\\ \hline \\ \end{array}
2) Multiply the top polynomial by each of the terms in the lower one.
Placing the results below.
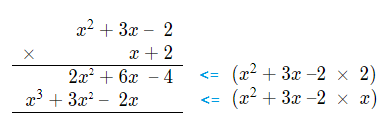
3) Add the results of these multiplications together for the solution to the initial sum.
\begin{array}{r} \space 2x^{\tt{2}} + 6x \space {\text{--}} \space 4\\ {\color{blue}+} \space\space\space\space x^{\tt{3}} + 3x^{\tt{2}} \space\space {\text{--}} \space 2x \space\space\space\space\space\space \\ \hline x^{\tiny{3}} + \space 5x^{\tiny{\tt{2}}} + 4x \space {\text{--}} \space 4\\ \end{array}
( x^{\tt{2}} + 3x \space {\text{--}} \space 2 ) \times ( x + 2 ) \space\space = \space\space x^{\tt{3}} + 5x^{\tt{2}} + 4x \space {\text{--}} \space 4
Multiplying Polynomials Examples
(1.1)
( 3x^{\tt{2}} + 5x \space {\text{--}} \space 2 ) \times ( x^{\tt{2}} + 4 )
Solution
\begin{array}{r} \space\space\space\space 3x^{\tt{2}} + 5x \space\space {\text{--}} \space 2\\ \times \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space x^{\tt{2}} + \space 0 \space + 4\\ \hline \space 12x^{\tiny{\tt{2}}} + 20x {\text{--}} \space 8\\ 3x^{\tt{4}} + 5x^{\tt{3}} \space {\text{--}} \space\space 2x^{\tiny{\tt{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \end{array}
=> \begin{array}{r} \space 12x^{\tiny{\tt{2}}} + 20x \space {\text{--}} \space 8\\ {\color{blue}+} \space\space\space\space x^{\tt{4}} + \space 5x^{\tt{3}} \space\space {\text{--}} \space\space\space 2x^{\tiny{\tt{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \hline x^{\tiny{4}} + \space 5x^{\tiny{3}} + 10x^{\tiny{\tt{2}}} + 20x \space {\text{--}} \space 8\\ \end{array}
Answer: ( 3x^{\tt{2}} + 5x \space {\text{--}} \space 2 ) \times ( x^{\tt{2}} + 4 ) \space\space = \space\space 3x^{\tt{4}} + \space 5x^{\tt{3}} + 10x^{\tt{2}} + 20x \space {\text{--}} \space 8
(1.2)
( a^{\tt{2}} + 8a \space {\text{--}} \space 3 ) \times ( 4a^{\tt{2}} \space {\text{--}} \space a + 2 )
Solution
Here there are 3 terms in each polynomial, the process we follow is the same, but there will be some more sums and terms to deal with.
There will three rows of multiplication results to add together for the final answer.
\begin{array}{r} \space\space\space\space a^{\tt{2}} + \space 8a \space {\text{--}} \space\space 3\\ \times \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 4a^{\tt{2}} \space\space {\text{--}} \space\space\space\space a + 2\\ \hline \space 2a^{\tiny{\tt{2}}} + 16a \space {\text{--}} \space 6\\ {\text{-}}a^{\tiny{3}} \space {\text{--}} \space\space 8a^{\tiny{2}} + \space\space 3a \space\space\space\space\space\space\\ 4a^{\tiny{4}} + 32a^{\tiny{3}} \space {\text{--}} \space 12a^{\tiny{\tiny{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \end{array}
=> \begin{array}{r} \space 2a^{\tiny{\tt{2}}} + 16a \space {\text{--}} \space 6\\ {\text{-}}a^{\tiny{3}} \space {\text{--}} \space\space 8a^{\tiny{2}} + \space\space 3a \space\space\space\space\space\space\\ {\color{blue}+} \space\space\space\space 4a^{\tiny{4}} + 32a^{\tiny{3}} \space {\text{--}} \space 12a^{\tiny{\tiny{2}}} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \\ \hline 4a^{\tiny{4}} + 31a^{\tiny{3}} \space {\text{--}} 18a^{\tiny{2}} + 19a \space {\text{--}} \space 6\\ \end{array}
Answer: ( a^{\tt{2}} + 8a \space {\text{--}} \space 3 ) \times ( 4a^{\tt{2}} \space {\text{--}} \space a + 2 ) \space\space = \space\space 4a^{\tt{4}} + \space 31a^{\tt{3}} \space {\text{--}} \space 18a^{\tt{2}} + 19a \space {\text{--}} \space 6