On this Page:
1. Exponential Functions
2. Logarithmic Functions
3. Logarithms, Base 10 and Base e
4. Logarithms Further
1. Exponential Functions
2. Logarithmic Functions
3. Logarithms, Base 10 and Base e
4. Logarithms Further
Here we will look at exponential and logarithmic functions, what they represent and how they relate to each other in Algebra.
Exponential Functions
If we have a function of the form f(x) = a^x, a > 0.
This is an exponential function.
The base number is a, and the exponent is x.
If we recall: 3^2 \space {\small{=}} \space 3 \times 3 \space {\small{=}} \space 9 , 3^3 \space {\small{=}} \space 3 \times 3 \times 3 \space {\small{=}} \space 27
Logarithmic Functions
A logarithm is a function that goes the other way from an exponential one.
It is the inverse function to the exponential function.
Such a function has the general form. f(x) \space {\small{=}} \space{\tt{log}}_a (x)
With a > 0 \space \space , \space \space a \space {\cancel{=}} \space 1 \space \space , \space \space x > 0. ( We’ll explain these conditions further in the page. )
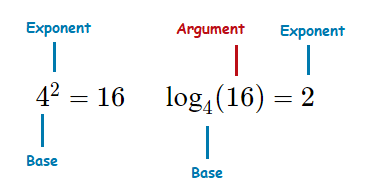
We know, 4^2 \space {\small{=}} \space 4 \times 4 \space {\small{=}} \space 16.
The base number is 4, the argument is x, and the exponent is 2.
As a logarithmic function we write, {\tt{log}}_4 (16) \space {\small{=}} \space 2.
So the result is, what does the base number a have to be raised to in order to get x.
It’s the case that exponential and logarithmic functions are inverses of each other.
One undoes the work of the other.
– {\tt{log}}_a (a^x) \space {\small{=}} \space x => a^{{\tt{log}}_a (x)} \space {\small{=}} \space x
So if we have, f(x) \space {\small{=}} \space{\tt{log}}_4 (x). Then, 4^{f(x)} \space {\small{=}} \space x.
Logarithms Explained, Base 10 and Base e
Logarithm Base 10
A logarithm with base 10 is known as a ‘common logarithm’. \boxed{{\tt{log}}_{10} (x)}
It’s the case that the ’10’ is generally left unwritten,
but is implied/assumed.
So when we encounter, {\tt{log}} (x).
This is assumed to be, {\tt{log}}_{10} (x).
‘{\tt{log}} (100)‘ would be assumed to be ‘{\tt{log}}_{10} (100)‘.
{\tt{log}} (100) \space {\small{=}} \space {\tt{log}}_{10} (100) \space {\small{=}} \space 2
The ‘log’ button on a calculator is the logarithm of base 10.
Logarithm Base e
A logarithm of base e is known as a ‘natural logarithm’. \boxed{{\tt{log}}_{e} (x)}
This logarithm is often written {\tt{ln}}(x),
{\tt{log}}_{e} (x) \space {\small{=}} \space {\tt{ln}} (x)
Like logarithms with base 10, the natural logarithm also appears as a button on a calculator.
If we wanted to find the natural logarithm of 825.
We can use a calculator to establish. {\tt{ln}}(825) \space {\small{=}} \space 6.715
For both the common logarithm and natural logarithm, it’s the case that:
10^{{\tt{log}}(x)} \space {\small{=}} \space x and e^{{\tt{ln}}(x)} \space {\small{=}} \space x.
Logarithms, 0, 1,
Negative Numbers and Decimals
Earlier in the page it was stated that for f(x) \space {\small{=}} \space{\tt{log}}_a (x).
We needed a > 0 \space \space , \space \space a \space {\cancel{=}} \space 1 \space \space , \space \space x > 0.
But why is this?
When we’re dealing with real numbers, certain issues occur when we don’t constrain the values of a and x.
Let’s look at them.
Base Value:
Can’t have 0.Having logarithms with base 0 would give us situations like the following.
{\tt{log}}_0 (2) \space {\small{=}} \space x => 0^x \space {\small{=}} \space 2
{\tt{log}}_0 (4) \space {\small{=}} \space x => 0^x \space {\small{=}} \space 4
Now 0 raised to any power is still 0, so this base can’t occur for a logarithm.
Can’t have 1.
Having logarithms with base 1 would give us situations like the following.
{\tt{log}}_1 (2) \space {\small{=}} \space x => 1^x \space {\small{=}} \space 2
{\tt{log}}_1 (12) \space {\small{=}} \space x => 1^x \space {\small{=}} \space 12
Now 1 raised to a power is still 1, so this base can’t occur for a logarithm.
Can’t be negative.
Having logarithms with negative base numbers would give us situations like the following.
{\tt{log}}_{{\text{--}}5} (x) \space {\small{=}} \space {\Large{\frac{1}{2}}} => {\text{--}}5^{\frac{1}{2}} \space {\small{=}} \space x => \sqrt{{\text{--}}5} \space {\small{=}} \space x
Now with real numbers we can’t take the root of a negative number, so this base couldn’t occur for a logarithm.
Argument:
Can’t be negative.
Having logarithms with negative argument numbers would give us situations like the following.
{\tt{log}}_{10} ({\text{--}}100) \space {\small{=}} \space x => 10^x \space {\small{=}} \space {\text{--}}100
The issue is that any real x will produce a positive result.
10^3 \space {\small{=}} \space 1000 , 10^{{\text{--}}3} \space {\small{=}} \space {\Large{\frac{1}{1000}}} , 10^0 \space {\small{=}} \space 1 etc
Can’t be Zero.
Having logarithms with a zero argument would give us situations like the following.
{\tt{log}}_{10} (0) \space {\small{=}} \space x => 10^x \space {\small{=}} \space 0
There isn’t an x value that can satisfy this result.
Outputs and Decimals:
To conclude this logarithms explained page, the output of a logarithm can be a negative number just fine.
For example.
{\tt{log}}_{5} (0.2) \space {\small{=}} \space {\text{-}}1 => 5^{{\text{--}}1} \space {\small{=}} \space {\Large{\frac{1}{5}}} \space {\small{=}} \space 0.2
We are also fine to use decimal numbers with logarithms, provided they satisfy the value constraints.
{\tt{log}}_{10} (14) \space {\small{=}} \space 1.146128... => 10^{1.146128...} \space {\small{=}} \space 14
{\tt{log}}_{10} (27) \space {\small{=}} \space 1.88649... => 10^{1.88649...} \space {\small{=}} \space 27