Intro to Matrices, Elements of a Matrix,
Notation

This intro to matrices page will aim to introduce the concept of a matrix in Math. Along with explaining about rows and columns in a matrix and how to label the elements of a matrix.

Intro to Matrices,
What is a Matrix in Math?

In Math, a matrix is a rectangular arrangement of information in rows and columns, the plural of matrix is matrices when you have more than one.
Matrices can have a range of applications in different disciplines.

Generally, a matrix is enclosed between either two square brackets or two curved brackets.

Each of the above are the same matrix, just presented with different brackets enclosing them.

The matrices we feature on this page and on this website will all use the square brackets in their presentation.

Matrix Rows and Columns, Notation

The rows of a matrix are vertical along the side, while the columns are horizontal along the top.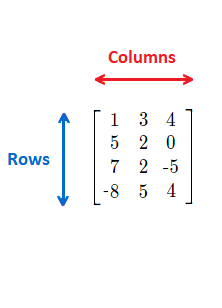

To describe the size of a matrix, we say ROWS by COLUMNS, on paper represented by an X between them.

A  =  \begin{bmatrix} 4 & {\text{-}}7 & 2 \\ 3 & 0 & 1 \\ 0 & 2 & {\text{-}}4 \end{bmatrix}           B  =  \begin{bmatrix} \space a & b \space \\ \space c & d \space \\ \space e & f \space \\ \end{bmatrix}


A  is a 3 by 3 matrix,  ( 3 x 3 ).         B  is a 3 by 2 matrix,  ( 3 x 2 ).

Matrices are usually denoted with a capital letter, such as matrix A and matrix B above.

Elements of a Matrix

The numbers or letters inside a matrix are called the ‘elements’ of the matrix.

While a matrix is denoted with a capital letter, an element is labelled with a corresponding small case letter, along with the relevant row and column position.

An element of a matrix  A  is written as  a_{ij}.
Where  i  is the row number, and  j  is the column number.


For the matrix     A  =  \begin{bmatrix} 4 & {\text{-}}7 & 2 \\ 3 & 0 & 1 \\ 0 & 2 & {\text{-}}4 \end{bmatrix}

The element  a₁₂  is  –7,  being 1 row down and 2 columns along.

While the element  a₃₂  is  2.  being 3 rows down and 2 columns along.

Transpose of a Matrix

With an intro to matrices, it’s important to know about how to transpose a given matrix.

We can ‘transpose’ a matrix in Math, which is the operation of flipping a matrix, where we switch around the rows and columns.

The notation for the transpose is a capital  T  to the top right of the original matrix.


So for the matrix  C  =  \begin{bmatrix} 1 & {\text{-}}4 \\ 6 & 9 \\ 5 & 6 \end{bmatrix}.         =>         \begin{bmatrix} 1 & {\text{-}}4 \\ 6 & 9 \\ 5 & 6 \end{bmatrix}^T  =  \begin{bmatrix} 1 & 6 & 5 \\ {\text{-}}4 & 9 & 6 \end{bmatrix}


In the original matrix  –4  was element  c₁₂.  In the transposed matrix, it is now element  c₂₁.
The rows and columns were switched around.

Main Diagonal of a Matrix

The main diagonal of a matrix is the diagonal from the top left element descending to the right one element at a time.

A matrix doesn’t have to be square to have a main diagonal.

Below are 3 matrices where the leading diagonal elements are in red.


\begin{bmatrix} {\color{red}4} & 7 & {\text{-}}2 \\ 3 & {\color{red}0} & 1 \\ 0 & 2 & {\color{red}{\text{-}}4} \end{bmatrix}     \begin{bmatrix} {\color{red}3} & 8 & {\text{-}}1 \\ 3 & {\color{red}5} & 1 \end{bmatrix}     \begin{bmatrix} {\color{red}2}& 0 & 1 \\ 3 & {\color{red}{\text{-}}6} & 4 \\ 0 & 8 & {\color{red}5} \\ 2 & {\text{-}}9 & 4 \end{bmatrix}


NOTE

The main diagonal of a matrix can also be called the ‘leading diagonal’, ‘major diagonal’, ‘principal diagonal’ or ‘primary diagonal’.

1. Home
 ›
2. Algebra 2
› Matrix Math Introduction

---

Return to TOP of page