In Math an interval is the range of all real numbers between two specific values,
where these values are classed as the end points of said interval.
We can express and represent intervals with suitable interval notation in Math.
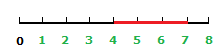
The red line on the number line drawn represents an interval between the numbers 4 and 7.
An interval like this, can be expressed and written in a couple of methods with interval notation, depending on the situation.
Interval Notation in Math
Open Interval:
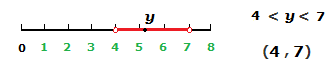
An open interval is written with curly brackets. (a,b)
An open interval is where the specific end points are NOT included in the interval itself.
The interval written above would contain every real number between a and b,
but NOT contain a and b themselves.
Which means any random value y has to be a number greater than a, but also smaller than b.
So (4,7) is the same as 4 < y < 7.
The hollow circles on the number line image where the end points are below, indicate that the end points are NOT contained within the interval.
Closed Interval:
A closed interval is written with square brackets. [a,b]
This is an interval that does contain the end points.
The interval includes every number between a and b, and a and b themselves.
Alternative notation can be a < y < b.
Which means that any number y within the interval, can be larger than or equal to a, and less than or equal to b.
So [2,6] is the same as 2 < y < 6.
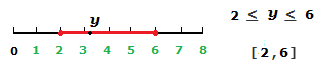
The filled in circles at the end points in the graph illustration, indicate that the end points are included in the interval.
Partly Open or Closed Interval:
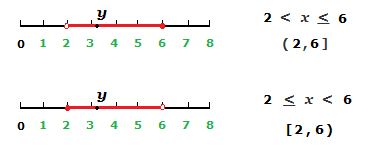
It’s the case that an interval doesn’t have to be solely open or closed. It can be a combination of both.
If we write an interval as (a,b]. This is an interval that includes the value of b, but doesn’t include value a.
Can also be notated as a < y < b,
So x has to be a value larger than b, but can be a value smaller than or equal to b.
(2,6] is equivalent to 2 < y < 6.
Now an interval written as [a,b), is an interval that includes the value a, but NOT b.
Can also be of the form a < y < b,
y has to be less than b, but can be greater than or equal to a.
Infinity and Interval Notation
Infinity is something that can appear in interval notation in Math too.
(-∞ , ∞) is the same as x ∈ ℜ.
We have y being a value of any real number.
Now each ∞ must be alongside a curly bracket in the interval notation,
because infinity isn’t really an exact end point of an interval.
There isn’t a specific finite end point value, infinity is something that goes on and on without an end, and has no exact numerical value.
So an interval can’t really include infinity within it as an end point, in the same way it can with a numerical value.
[–∞ , ∞] is INCORRECT, (–∞ , ∞) is CORRECT.
y > 3 is equivalent to (3 , ∞).
y can’t be 3, or less than 3. But can be any real number larger than 3.
y > 3 is the same as [3 , ∞).
y can be the number 3, or also any real number greater than 3.
Situations that are similar can also be expressed in the same way with –∞.
