In Math a ratio is an effective method of comparing different values of certain things. Enabling us to see how much of some quantity there is compared to another quantity of the same measurement.
This page will demonstrate how ratios work, and show how to write ratios, and how they can help compare values such as lengths, weights and areas.
The units of measure used for a comparison in a ratio do need to be the same.
Introduction, How to Write Ratios
Say a clothes drawer contains 5 shirts.
Inside the drawer are 3 red shirts and 2 red shirts.
3 RED SHIRTS
2 BLUE SHIRTS
The ratio of red shirts to blue shirts is 3 : 2.
There are 4 times as many red shirts as there are yellow shirts.
Notation:
a : b is the common general notation for Ratios.Though sometimes we can see that ratios can be represented as a fraction also, {\frac{\tt{a}}{\tt{b}}}.
So with the red and blue shirt ratio above could also be written as, \bf{\frac{3}{2}}.
Also, the ratio could if one wished, be written in a different order,
perhaps as blue shirts to red shirts instead, 2 : 3.
Ratio, Simplified Ratios:
The ratio 3 : 2 doesn’t only have to represent a group/collection of 5 things though, such as in the case earlier with the shirts.
A ratio can be a what is known as a simplified ratio, representing a group that is larger than 5 in size.
If the drawer contained 6 red shirts and 2 blue shirts.
Then the ratio of red shirts to blue shirts would be 6 red shirts to 2 blue shirts,
6 : 2 which can be simplified further to 3 : 1.
Even in this drawer with more shirts, the ratio is still 3 : 1.
As there is still 3 times as many red shirts as blue shirts overall.
Like in the case with fractions, ratios are often simplified where possible to a neater and tidier equivalent ratio.
For example 16 : 4 and 4 : 1 are equivalent ratios, because they represent the same scale.
Writing Ratios Examples
(1.1)
Express 8 : 40 as a ratio in its simplest form.
Solution
Largest common factor of both numbers is 8.
8 ÷ 8 = 1 , 40 ÷ 8 = 5
8 : 40 can be simplified to 1 : 5
(1.2)
Express 27 : 9 as a ratio in its simplest form.
Solution
27 ÷ 9 = 3 , 9 ÷ 9 = 1
27 : 9 can be simplified to 3 : 1
(1.3)
Express 1 YEAR to 10 MONTHS as a ratio in its simplest form.
Solution
1 YEAR : 10 MONTHS
We first look to make both measurements/units in the ratio the same.
They aren’t initially in this example, as a year and a month are different values.
Something we can do is to change 1 YEAR into 12 MONTHS.
1 YEAR : 10 MONTHS = 12 MONTHS : 10 MONTHS = 12 : 10
Now the ratio 12 : 10 can now be simplified to 6 : 5
(1.4)
Share $3000 in the ratio 2 : 3.
Solution
2 : 3 is 5 parts in total.
As a first step we split $3000 into 5 equal parts.
$3000 ÷ 5 = $600
Sometimes it can be helpful to draw a suitable number line to illustrate the example and understand what’s going on visually.
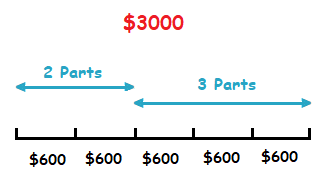
2 parts = $1200 , 3 parts = $1800
So for $3000:
The ratio 2 : 3 = $1200 : $1800
Ratios, another case
There can be the case that sometimes a ratio can represent a part of a smaller group, to a greater whole group.
Part of Group : Larger Whole Group
With the shirts in the drawer example, the 3 red shirts alone, could be written as the ratio 3 : 5.
Representing that there is 4 red shirts in the drawer, in relation to all shirts that in the drawer in total.
Example
(2.1)
An oil barrel has a capacity of 40 gallons, but has only been filled with 10 gallons of oil.
What ratio of the barrel has been filled with oil.
Solution
Part of Group : Larger Whole Group = 10 : 40
10 : 40 can be simplified to the ratio 1 : 4
Or if we wanted to represent the ratio in fraction form.
\boldsymbol{\tt\frac{Part \space of \space Group}{Larger \space Whole \space Group}} = \bf{\frac{10}{40}} = \bf{\frac{1}{4}}
\bf{\frac{1}{4}} of the barrel has been filled with oil.