When learning how to write compound inequalities, it’s important to first understand exactly what a compound inequality is.
A compound inequality is a kind of double inequality
, where there are 2 inequalities present instead of just 1.
A compound inequality is where 2 inequalities are connected by the word “and” or the word “or”.
When the word “and” is present, the solution is any value that makes both inequalities true.
When the word “or” is present, the solution is any value that makes either inequality true.
Writing Compound Inequalities:
If we have 2 inequalities present such as x \gt {\text{-}}2 , x \lt 2.
This can be combined and written as a double inequality, {\text{-}}2 \lt x \lt 2.
But if two inequalities present were x \lt {\text{-}}3 , x \gt 4.
We can’t write, 4 \lt x \lt {\text{-}}3.
As a value can’t be less than -3 as well as being greater than 4.
But we can write, x \lt {\text{-}}3 or x \gt 4.
It turns out that many compound inequalities where the word “and” would be present, can in fact be written as a double inequality, or even a single inequality.
x \le 9 and x \gt 5 can be written, 5 \lt x \le 9.
x \le 9 and x \lt 12 can be written as just, x \le 9.
How to Write Compound Inequalities,
Solving Examples
(1.1)
Solve 5x \space {\text{--}} \space 3 \lt 8 or 2x + 5 \ge 9.
Solution
We deal with each inequality separately on their respective side.
5x \space {\text{--}} \space 3 + 3 \space\lt \space 8 + 3 or 2x + 5 \space {\text{--}} \space 5 \space \ge \space 9 \space {\text{--}} \space 5
5x \lt 5 or 2x \ge 4
\frac{5x}{5} \lt \frac{5}{5} or \frac{2x}{2} \ge \frac{4}{2}
x \lt 1 or x \ge 2
For the graph of such an inequality, we look at the graphs separately, then combine them.
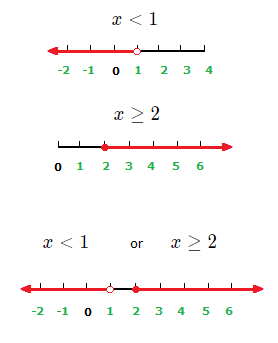
(1.2)
Solve 4a \space {\text{--}} \space 9 \lt {\text{-}}21 or {\text{-}}a + 6 \le 1.
Solution
4a \space {\text{--}} \space 9 + 9 \lt {\text{-}}21 + 9 or {\text{-}}a + 6 \space {\text{--}} \space 6 \le 1 \space {\text{--}} \space 6
4a \lt {\text{-}}12 or {\text{-}}a \le {\text{-}}5
\frac{4a}{4} \lt \frac{{\text{-}}12}{4} or {\text{-}}a \times ({\text{-}}1) \space \le \space {\text{-}}5 \times ({\text{-}}1)
a \lt {\text{-}}3 or a \ge 5
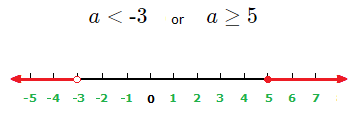
(1.3)
Solve 5x + 2 \le 12 and x + 2 \gt 3.
Solution
5x + 2 \space {\text{--}} \space 2 \le 12 \space {\text{--}} \space 2 and x + 2 \space {\text{--}} \space 2 \gt 3 \space {\text{--}} \space 2
5x \le 10 and x \gt 1
\frac{5x}{5} \le \frac{10}{5} and x \gt 1
x \le 2 and x \gt 1
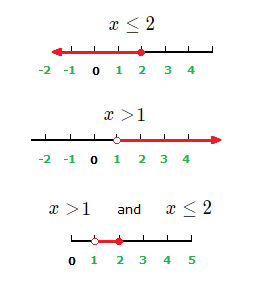
(1.4)
Solve 1 + 4x \le 9 and {\text{-}}3x \space {\text{--}} \space 4 \gt {\text{-}}16.
Solution
1 \space {\text{--}} \space 1 + 4x \le 9 \space {\text{--}} \space 1 and {\text{-}}3x \space {\text{--}} \space 4 + 4 \gt {\text{-}}16 + 4
4x \le 8 and {\text{-}}3x \gt {\text{-}}12
\frac{4x}{4} \le \frac{8}{4} and \frac{{\text{-}}3x}{{\text{-}}3} \gt \frac{{\text{-}}12}{{\text{-}}3}
x \le 2 and x \lt 4
Which in fact can be written as just the single inequality x \le 2.
As a value less than or equal to 2, will also be less than 4.
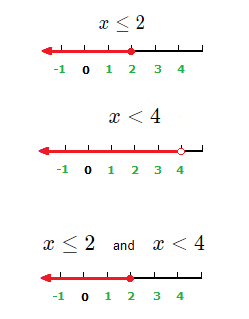
(1.5)
Solve 3x \space \le \space x + 2 \space \lt \space 2x + 5.
Solution
Now this may initially be the form of a double inequality. But for a double inequality such as this where a variable is in each part.
We can split it up into a compound inequality, and proceed with solving.
3x \space \le \space x + 2 and x + 2 \space \lt \space 2x + 5
3x \space {\text{--}} \space x \space \le \space x + 2 \space {\text{--}} \space x and x + 2 \space {\text{--}} \space x \space \lt \space 2x + 5 \space {\text{--}} \space x
2x \space \le \space 2 and 2 \space \lt \space x + 5
\frac{2x}{2} \le \frac{2}{2} and {\text{-}}x \lt {\text{-}}2 + 5
x \le 1 and {\text{-}}x \lt 3
x \le 1 and x \gt {\text{-}}3