When multiplying two binomials together, we can use what is known as FOIL method multiplication. This method is used when expanding brackets involving binomials is required.
The adding and multiplying algebraic expressions page showed an example of vertical multiplication involving two binomials, but the FOIL method can sometimes be more suitable.
FOIL method multiplication is a further development from when we multiply a binomial by just a number, for example:
3(x + 2)
This multiplication happens in 2 steps.
First is 3 \times x, then 3 \times 2, before adding.
So 3(x + 2) \space = \space 3x + 6.
More generally a(b \pm c) \space = \space ab \plusmn ac
With FOIL multiplication we follow on from this.
FOIL Method Multiplication Steps:
We can consider a basic example involving two binomials in brackets to be multiplied together.(x + 3)(x \space {\text{--}} \space 4)
This multiplication is done in 4 steps, which is where the word FOIL comes from for these situations in Math.
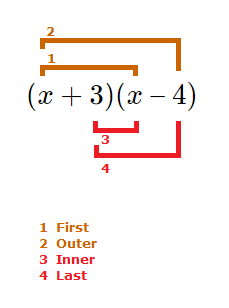
As the diagram above shows, the 4 steps to FOIL method multiplication are:
First , Outer , Inner , Last
Hence the name FOIL multiplication.
The word is an easy and quick way to remember the correct steps in which to the multiplication when multiplying two binomials together.
So for the multiplication of the binomials in the image we have.
(x + 3)(x \space {\text{--}} \space 4)
‘First’ => x \times x , ‘Outer’ => x \times {\text{-}}4
‘Inner’ => 3 \times x , ‘Last’ => 3 \times {\text{-}}4
Now we add the four multiplication results together and combine any like terms.
x^2 \space {\text{--}} \space 4x + 3x + 12 \space = \space x^2 \space {\text{--}} \space x + 12
So we have: (x + 3)(x \space {\text{--}} \space 4) \space = \space x^2 \space {\text{--}} \space x + 12.
General case: \bf{(a \pm b)(c \pm d) \space = \space ac \pm ad \pm bc \pm bd}
Examples
(1.1)
Expand (x + 5)(x + 3).
Solution
(x + 5)(x + 3) \space = \space x^2 + 3x + 5x + 15
= \space x^2 + 8x + 15
(1.2)
Expand (x \space {\text{--}} \space 1)(x \space {\text{--}} \space 4).
Solution
(x \space {\text{--}} \space 1)(x \space {\text{--}} \space 4) \space = \space x^2 \space {\text{--}} \space 4x \space {\text{--}} \space x + 4
= \space x^2 \space {\text{--}} \space 5x + 4
(1.3)
Multiply out ({\text{-}}x + 6)(x \space {\text{--}} \space 3).
Solution
({\text{-}}x + 6)(x \space {\text{--}} \space 3) \space = \space {\text{-}}x^2 \space {\text{--}} \space 3x + 6x \space {\text{--}} \space 18
= \space {\text{-}}x^2 + 3x \space {\text{--}} \space 18