Find the Sample Standard Deviation

Along with finding the complete  standard deviation  of a set of data, we can also find the sample standard deviation if we wished.


The sample standard deviation is a measurement that is very useful for times when you would like to get a good idea of the standard deviation of a perhaps a very large group, but without having to use all the values in the whole group.

Now there was a formula for complete standard deviation, and there is also a formula for sample standard deviation that can be used.

Sample Standard Deviation Formula

The formula for the sample standard deviation is the following.

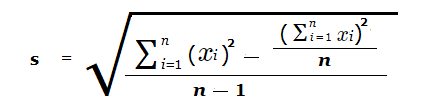
Where we have &nbspn&nbsp being the size of the sample of data, and not the size of the whole complete group.

---

Standard Deviation and
Sample Standard Deviation Comparison

To show sample standard deviation in practice, we can look at a random list of &nbsp10&nbsp numbers.

We will work out the complete standard deviation, then proceed to work out a sample standard deviation from just some of the &nbsp10&nbsp numbers.

List of &nbsp10&nbsp numbers: &nbsp &nbsp 7 , 11 , 14 , 12 , 9 , 10 , 8 , 9 , 12 , 18

Total amount of values. &nbsp n &nbsp=&nbsp 10

Average/mean ( μ ) &nbsp=&nbsp \bf{\frac{7 \space + \space 11 \space + \space 14 \space + \space 12 \space + \space 9 \space + \space 10 \space + \space 8 \space + \space 9 \space + \space 12 \space + \space 18}{10}} &nbsp=&nbsp 11

Standard Deviation:

Standard Deviation &nbsp = &nbsp \sqrt{\frac{\sum_{i=1}^n \space (x_i)^2}{n} \space – \space \mu^2}

= &nbsp \bf{\sqrt{\frac{7^2 \space + \space 11^2 \space + \space 14^2 \space + \space 12^2 \space + \space 9^2 \space + \space 10^2 \space + \space 8^2 \space + \space 9^2 \space + \space 12^2 \space + \space 18^2}{10} \space {\text{–}} \space 11^2}}

= &nbsp \bf{\sqrt{130.4 \space – \space 121}} &nbsp = &nbsp \bf{\sqrt{9.4}} &nbsp = &nbsp 3.07 &nbsp &nbsp ( to 2 decimal places )



Looking at a range &nbsp1&nbsp standard deviation away from the mean:

11 − 3.07 &nbsp=&nbsp 7.93 &nbsp , &nbsp 11 + 3.07 &nbsp=&nbsp 14.07

So we should expect that the majority of the values in the list of numbers would be between &nbsp7.93&nbsp and &nbsp14.07.

This does turn out to be the case, as only &nbsp18&nbsp happens to lie outside the range of one standard deviation away from the mean/average.

Sample Standard Deviation:

Now we will look to take a sample standard deviation, using &nbsp5&nbsp of the &nbsp10&nbsp numbers as a sample.


Selection of &nbsp5&nbsp numbers from the list: &nbsp &nbsp 7 , 8 , 9 , 10 , 18

Amount of values. &nbsp n &nbsp=&nbsp 5

Average/mean ( μ ) &nbsp=&nbsp \bf{\frac{7 \space + \space 8 \space + \space 9 \space + \space 10 \space + \space 18}{5}} &nbsp=&nbsp 10.4


Sample Standard Deviation &nbsp=&nbsp \sqrt{\frac{\sum_{i=1}^n \space (x_i)^2 \space {\text{–}} \space {\frac{(\sum_{i=1}^nx_i)^2}{n}}}{n \space {\text{–}} \space 1}}


= &nbsp \bf{\sqrt{\frac{(49 \space + 64 \space + \space 81 \space + \space 100 \space + \space 324) \space {\text{–}} \space {\frac{2704}{5}}}{4}}} &nbsp=&nbsp \bf{\sqrt{19.3}} &nbsp=&nbsp 4.39



Again now looking at a range of &nbsp1&nbsp sample standard deviation away from the sample mean/average.

10.04 − 4.39 &nbsp=&nbsp 5.65 &nbsp &nbsp , &nbsp &nbsp 10.04 + 4.39 &nbsp=&nbsp 14.43

Result

These new calculations to find the sample standard deviation, indicate we should expect most of the values in the complete list of &nbsp10&nbsp numbers to be between &nbsp5.65&nbsp and &nbsp14.43.


Again this does turn out to be the case, as it is still only &nbsp18&nbsp that lies outside this range in the whole complete list

So the Sample Standard Deviation does still give a fairly accurate result for the larger group.

---

Find the Sample Standard Deviation
Example

(1.1)&nbsp

A person who plays golf at a country club with &nbsp100&nbsp members, would like to know roughly how many rounds each member played in one week.

They want to get a good measure of how spread out the results would likely be.

Instead of asking all &nbsp100&nbsp members, the person decides to take a random sample of &nbsp9&nbsp members.

In order to get an idea of what the rounds played results would likely be for the whole &nbsp100&nbsp members.



The number of rounds played for sample of &nbsp7&nbsp members were:

1 , 4 , 2 , 2 , 5 , 8 , 3 , 2 , 3



Mean &nbsp = &nbsp \bf{\frac{1 \space + \space 4 \space + \space 2 \space + \space 2 \space + \space 5 \space + \space 8 \space + \space 3 \space + \space 2 \space + \space 3}{9}} &nbsp=&nbsp \bf{\frac{26}{9}} &nbsp=&nbsp 2.89 &nbsp &nbsp , &nbsp &nbsp n &nbsp=&nbsp 9

Now to obtain the Sample Standard Deviation &nbsps&nbsp with these values.

s &nbsp = &nbsp \bf{\sqrt{\frac{1^2 \space + \space 2^2 \space + \space 2^2 \space + \space 2^2 \space + \space 3^2 \space + \space 3^2 \space + \space 4^2 \space + \space5^2 \space + \space 8^2 \space \space {\text{–}} \space \space {\frac{(30)^2}{9}}}{9 \space {\text{–}} \space 1}}}

=&nbsp \bf{\sqrt{\frac{136 \space \space {\text{–}} \space \space {\frac{900}{9}}}{8}}} &nbsp=&nbsp \bf{\sqrt{\frac{36}{8}}} &nbsp&nbsp \bf{\sqrt{4.5}} &nbsp=&nbsp 2.12


2.89 − 2.12 &nbsp=&nbsp 0.77 &nbsp &nbsp , &nbsp &nbsp 2.89 + 2.12 = 5.01

From the results of the sample of &nbsp9&nbsp club members.

It’s reasonable to assume that for the whole group of &nbsp100&nbsp club memebers:

The average number of rounds played in the one week studied should be around &nbsp3.

With the majority of the rounds played results being between &nbsp0.77&nbsp and 5.01.
So effectively between &nbsp1&nbsp and &nbsp5&nbsp rounds played.

1. Home
 ›
2. Probability and Statistics
› Sample Standard Deviation

---

Return to TOP of page