Before focusing on the zeros/roots of a polynomial, it’s best to have a full understanding of factors of polynomials.
The factoring quadratics page introduced factors of quadratics where there are generally 3 terms present, but we can also learn how to approach factoring polynomials with 4 terms.
With larger polynomials, the same logic follows on from factoring and solving quadratics. We have effective ways of factoring polynomials of degree 3.
When we obtain a factor of a polynomial (x \space {\text{–}} \space t), then x = t is a solution to the polynomial.
On a Graph
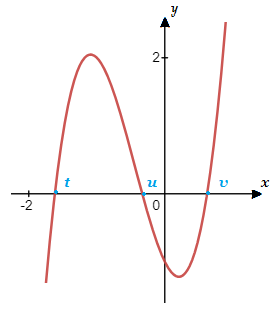
If we have a polynomial, f(x) = \space a_nx^n \space + \space a_{n \space {\text{–}} \space 1}x^{n \space {\text{–}} \space 1} \space + ….. + \space a_{\tt{2}}x^{\tt{2}} \space \space + a_1x \space + \space a_0and we can find the real number factors, f(x) = (x \space {\text{–}} \space t)(x \space {\text{–}} \space u)(x \space {\text{–}} \space v)…...
Then the values values of t, u, v ….
where (x \space {\text{–}} \space t) = 0 \space\space , \space\space (x \space\space {\text{–}} \space u) = 0 \space\space , \space\space (x \space {\text{–}} \space v) = 0 \space …..
will be the roots\zeros of the polynomial.
Degree of Polynomial:
The number of factors a polynomial has will be indicated by the ‘degree’ of the polynomial, which is the highest power/index of a variable that is present.2x + 3 is a polynomial of degree 1.
x^2 + 2x \space {\text{–}} \space 1 is a polynomial of degree 2.
x^3 + 5x^2 \space {\text{–}} \space 3x + 7 is a polynomial of degree 3, and so on.
Factoring Polynomials of Degree 2:
Polynomials of degree 2 are quadratics, and factors of quadratics was covered here.But we can give a brief recap.
An example of a quadratic polynomial of degree 2 is, x^2 + 2x \space {\text{–}} \space 3.
This can be factored into (x + 3)(x \space {\text{–}} \space 1).
Two factors as expected, from the polynomial degree.
Factoring Polynomials of Degree 3
When a polynomial is of degree 3 or larger, it can take a bit longer and be a bit more involved finding the factors and zeros.
Focusing on a polynomial of degree 3 here, we can introduce the general process when approaching such situations.
A polynomial we can consider is, 2x^3 + 3x^2 \space {\text{–}} \space 5x \space {\text{–}} \space 6.
We’ll state the factors just now before showing how to obtain them further down.
They are, (x + 2)(x + 1)(2x \space {\text{–}} \space 3).
A common and effective method of factoring polynomials of degree 3 and larger, is by synthetic division.
As when we obtain a remainder of 0, the value we are dividing by will be factor of the polynomial.
The rational roots test shown here can tell us what values to try initially with synthetic division.
But we’ve stated that (x + 1) is a factor, so we can proceed with synthetic division using the value of -1.
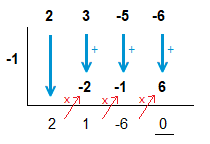
We obtained a remainder of 0 as expected for a factor of the polynomial.
But there is more to the story here, if we look at the terms below which we form into a new polynomial of a degree lower than the original.
This actually factors into the other two factors of the original polynomial.
2x^2 + x \space {\text{–}} \space 6 \space = \space (2x \space {\text{–}} \space 3)(x + 2)
Example
We’ll look to find the factors of p(x) = 2x^3 \space {\text{–}} \space 9x^2 \space {\text{–}} \space 2x + 24.
The remainder theorem can help us initially.
From the fact that when a polynomial p(x) is divided by (x \space {\text{–}} \space t),
when a remainder r is obtained, p(t) = r.
So if we input a value into the polynomial 2x^3 \space {\text{–}} \space 9x^2 \space {\text{–}} \space 2x + 24.
If we obtain a result of 0, then the value we have input will give us a factor.
We can try some initial guesses for possible factors and see if we get a zero result.
1st guess:
(x + 1), which means inputting -1.
p({\text{-}}1) = 2({\text{-}}1)^3 \space {\text{–}} \space 9({\text{-}}1)^2 \space {\text{–}} \space 2({\text{-}}1) + 24 \space = \space {\text{-}}2 \space {\text{–}} \space 9 + 2 + 24 \space = \space 15 ( Not zero )
2nd guess:
(x \space {\text{–}} \space 1), which means inputting 1.
p(1) = 2(1)^3 \space {\text{–}} \space 9(1)^2 \space {\text{–}} \space 2(1) + 24 \space = \space 2 \space {\text{–}} \space 9 \space {\text{–}} \space 2 + 24 \space = \space 15 ( Not zero )
3rd guess:
(x \space {\text{–}} \space 2), which means inputting 2.
p(1) = 2(2)^3 \space {\text{–}} \space 9(2)^2 \space {\text{–}} \space 2(2) + 24 \space = \space 16 \space {\text{–}} \space 36 \space {\text{–}} \space 4 + 24 \space = \space 0
With a remainder of 0 obtained, we can say that (x \space {\text{–}} \space 2) is a factor.
Now dividing p(x) by (x \space {\text{–}} \space 2) can help us to find the other factors.
We can again use synthetic division.
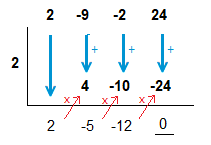
(2x^2 \space {\text{–}} \space 5x \space {\text{–}} \space 12)(x \space {\text{–}} \space 2)
=> (2x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space \space \space \space )(x \space {\text{–}} \space 2)
=> (2x + 3)(x \space {\text{–}} \space 4 )(x \space {\text{–}} \space 2)