Literal equations in Math are equations that contain more than one variable, which are letters generally in examples of literal equations.
The formula for the circumference of a circle is a literal equation where there are two variables.
C for the circumference and d for the diameter of the circle. C = πd
Attempting to solve literal equations examples involves rearranging and moving parts of the initial equation around, in order for the equation to then be expressed in terms of another variable.
So if we wanted to rewrite our circle circumference equation in terms of the diameter d,
division of both sides by π would achieve this.
So we can deduce that a circle diameter is given by division of the circumference by π.
Examples
(1.1)
The perimeter of a square with sides labelled g is given by: P = 4g.
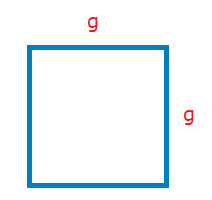
Solve the equation for g.
Solution
4g = P , {\frac{4g}{4}} = {\frac{P}{4}}
g = {\frac{P}{4}}
(1.2)
Solve 5c − d = e for d.
Solution
5c − d = e
We can move 5c across initially, making sure to change the nature.
–d = –5c + e
Now multiplying the equation all by -1 will give us the equation in terms of d.
–d = –5c + e ( × -1 ) => d = 5c − e
(1.3)
Solve R = 3s + 6t for s.
Solution
Subtracting 6t from both sides will give an expression in terms of s.
R − 6t = 3s + 6t − 6t => R − 6t = 3s
Now dividing through by 3 will solve for s.
{\frac{R - t}{3}} = {\frac{3s}{3}} => {\frac{R - t}{3}} = s
Examples of Literal Equations, Further
(2.1)
Solve C = {\frac{a}{4}}( b + 2 ) for b.
Solution
With literal equations examples like this one. Multiplying both sides by 4 will start us off by eliminating the fraction in the initial equation.
C = {\frac{a}{4}}( b + 2 ) ( × 4 ) => 4C = a( b + 2 )
Now we can multiply out the brackets and proceed.
4C = ab + 2a
{\frac{4C}{a}} = b + 2
{\frac{4C}{a}} − 2 = b
(2.2)
The equation for the area of an equilateral triangle with sides labelled a is A = {\frac{{\sqrt{3}}a^2}{4}}
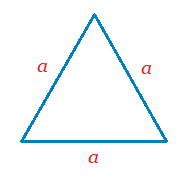
Express in terms of a.
Solution
A = {\frac{{\sqrt{3}}a^2}{4}} ( × 4 ) => 4A = {{\sqrt{3}}a^2}
We can now divide both sides by {\sqrt{3}}, giving us a^2.
{\frac{4A}{\sqrt{3}}} = a^2
To get the equation in terms of a, we now take the square root of both sides, as \sqrt{a^2} \space = \space a
\sqrt{{\frac{4A}{\sqrt{3}}}} = \sqrt{a^2} => \sqrt{{\frac{4A}{\sqrt{3}}}} = a