At times when we want to solve examples of dividing fractions, the main idea is really the same as when we’re dealing with division that involves whole numbers.
For example when you divide the number 12 by the number 4, you’re working out how many 4‘s there are in 12.
Now in a similar way, if you were to divide the fraction \bf{\frac{5}{7}} by the fraction \bf{\frac{1}{4}},
this is finding out how many \bf{\frac{1}{4}}‘s there are in \bf{\frac{5}{7}}.
How to divide Fractions:
A good thing is that dividing fractions shares similarities with multiplying fractions.
If one is able to understand the process of multiplying fractions, then learning how to divide fractions should pose no added problem.
When the situation requires dividing a fraction by a fraction, what you want to do is flip the dividing fraction upside down, and then multiply both the fractions together.
We can see how this process works in some dividing fractions examples below.
Examples
(1.1)
\bf{\frac{1}{3}} ÷ \bf{\frac{2}{5}} = \bf{\frac{1}{3}} × \bf{\frac{5}{2}} = \bf{\frac{5}{6}}
(1.2)
\bf{\frac{7}{10}} ÷ \bf{\frac{9}{16}} = \bf{\frac{7}{10}} × \bf{\frac{16}{9}} = \bf{\frac{112}{90}} = \bf{\frac{56}{45}}
(1.3)
\bf{\frac{8}{5}} ÷ \bf{\frac{1}{2}} = \bf{\frac{8}{5}} × \bf{\frac{2}{1}} = \bf{\frac{16}{5}}
(1.4)
3 ÷ \bf{\frac{4}{5}} = \bf{\frac{3}{1}} ÷ \bf{\frac{4}{5}} = \bf{\frac{3}{1}} × \bf{\frac{5}{4}} = \bf{\frac{15}{4}}
Dividing Mixed Fractions Examples
Like in the case of multiplying mixed fractions.
When dividing fractions examples involve mixed fractions, it’s usually best to convert the mixed fractions present into improper fraction form first.
How to do this is shown on the mixed numbers and fractions page.
Examples
(2.1)
3\bf{\frac{1}{5}} ÷ 1\bf{\frac{3}{4}} = \bf{\frac{16}{5}} ÷ \bf{\frac{7}{4}} = \bf{\frac{16}{5}} × \bf{\frac{4}{7}} = \bf{\frac{64}{35}} = 1\bf{\frac{29}{35}}
(2.2)
2\bf{\frac{1}{2}} ÷ 3\bf{\frac{4}{5}} = \bf{\frac{5}{2}} ÷ \bf{\frac{19}{5}} = \bf{\frac{5}{2}} × \bf{\frac{5}{19}} = \bf{\frac{25}{38}}
Examples of Dividing Fractions,
Complex Fractions
Slightly more advanced examples of dividing fractions than those already seen on this page can often involve what is known as “complex fractions”.
Complex fractions in Math are fractions where one of either the numerator or the denominator in the fraction also happen to be fractions themselves.
There are also times when both the numerator and the denominator can both be fractions, and not just one of them.
Below are some examples of typical standard complex fractions.
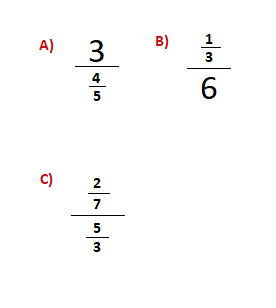
Complex Fractions in Sums:
Sums that involve complex fractions generally involve simplifying or converting the complex fraction to a simpler fraction or a whole number at some point.
Examples
(3.1)
Simplify the complex fraction \bf{\frac{6}{\tiny\frac{1}{2}}} as much as possible.
Solution
This fraction can be looked at as 6 ÷ \bf{\frac{1}{2}}.
Which is the same as \bf{\frac{6}{1}} ÷ \bf{\frac{1}{2}}.
Now: \bf{\frac{6}{1}} ÷ \bf{\frac{1}{2}} = \bf{\frac{6}{1}} × \bf{\frac{2}{1}} = \bf{\frac{12}{1}} = 12
(3.2)
Simplify the complex fraction \bf{\frac{16}{\tiny\frac{5}{3}}}.
Solution
Again thinking of \bf{\frac{16}{1}} ÷ \bf{\frac{5}{3}}.
\bf{\frac{16}{1}} ÷ \bf{\frac{5}{3}} = \bf{\frac{16}{1}} × \bf{\frac{3}{5}} = \bf{\frac{48}{5}}
(3.3)
Simplify the complex fraction \bf{\frac{\tiny\frac{2}{3}}{5}}.
Solution
\bf{\frac{2}{3}} ÷ 5 = \bf{\frac{2}{3}} ÷ \bf{\frac{5}{1}},
\bf{\frac{2}{3}} ÷ \bf{\frac{5}{1}} = \bf{\frac{2}{3}} × \bf{\frac{1}{5}} = \bf{\frac{2}{15}}
(3.4)
Simplify the complex fraction \bf{\frac{\tiny\frac{5}{8}}{\tiny\frac{3}{10}}}.
Solution
\bf{\frac{5}{8}} ÷ \bf{\frac{3}{10}} = \bf{\frac{5}{8}} × \bf{\frac{10}{3}} = \bf{\frac{50}{24}} = \bf{\frac{25}{12}}
- Home ›
- Fractions/Decimals › Dividing Fractions