The discriminant of a quadratic equation is something that can tell us the nature of the roots of the quadratic before we actually solve and find the roots.
The quadratic formula page showed how to solve quadratic equations and obtain roots using the quadratic formula.
The sum to work out the discriminant is part of this quadratic formula.
If we recall the quadratic formula. {\scriptsize{x = \space}} {\boldsymbol{\frac{{\text{-}}b \space \pm \space \sqrt{b^{2} \space - \space 4ac}}{2a}}}
The expression for the discriminant is the part inside the square root. \boxed{\boldsymbol{{b^{2}} - 4ac}}
This can be used to tell us the type of roots a standard quadratic equation of the form
ax^{\tt{2}} + bx + c = 0 will have.
Different Discriminant Values
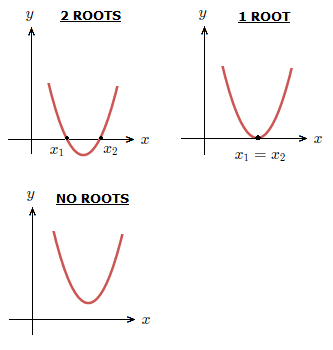
The value of the discriminant of a quadratic equation represents the following.\boldsymbol{{b^{2}} - 4ac} > 0 There are two different real roots.
\boldsymbol{{b^{2}} - 4ac} = 0 There are two equal real roots, so one root in total.
\boldsymbol{{b^{2}} - 4ac} < 0 There are no real roots, instead there are complex solutions.
We can show what these situations look like for a quadratic in graph form.
Discriminant of a Quadratic Examples
(1.1)
How many roots does the quadratic equation 2x^{\tt{2}} + 2x \space {\text{--}} \space 12 = 0 have.
Solution
Here: a = 2 \space \space , \space \space b = 2 \space \space , \space \space c = {\text{-}}12.
\boldsymbol{{b^{2}} - 4ac} = \space {2^{2}} \space {\text{--}} \space ( 4 \times 1 \times ({\text{-}}12) ) \space = \space 4 \space {\text{--}} \space ({\text{-}}48) \space = \space 52
As the discriminant is a positive number,
the quadratic equation 2x^{\tt{2}} + 2x \space {\text{--}} \space 12 = 0 has two distinct real roots.
We can actually neatly factor this quadratic equation if obtaining the roots were required.
2x^{\tt{2}} + 2x \space {\text{--}} \space 12 = 0 when factored becomes (2x \space {\text{--}} \space 4)(x + 3) = 0.
Giving the roots/solutions x = 2 \space , \space x = {\text{-}}3.
(1.2)
Determine if the roots of x^{\tt{2}} + 5x + 8 = 0 are equal, distinct or complex.
Solution
\boldsymbol{{b^{2}} - 4ac} = \space {5^{2}} \space {\text{--}} \space ( 4 \times 1 \times 8) ) \space = \space 25 \space {\text{--}} \space 32 \space = \space {\text{-}}7
As the value of the discriminant is negative, the roots of the quadratic equation will be complex.
(1.3)
What is the value of b if x^{\tt{2}} + bx + 9 = 0 has only one real root.
Solution
For the equation to have only one root, which is equal roots, the discriminant of a quadratic must be equal to zero.
{\boldsymbol{{b^{2}} - 4ac}} \space = \space b^{2} \space {\text{--}} \space (4 \times 1 \times 9) \space = \space b^{2} \space {\text{--}} \space 36
We want b^{2} \space {\text{--}} \space 36 to be zero.
b^{2} \space {\text{--}} \space 36 = 0 => b^{2} = 36
{\sqrt{b^{2}}} = {\sqrt{36}}
b = 6