Prior to learning about how to establish the inverse of a given matrix, something to learn about is the ‘determinant‘ of a square matrix.
The determinant is a real number that can be obtained from the elements of a square matrix, it can be a positive number or a negative number.
To find the determinant of a matrix that is square of size 2 x 2 and 3 x 3 in particular,
the determinant can be obtained performing calculations using a matrix determinant formula.
The common notation for the determinant is, det( A ) or | A |.
While the determinant of a square matrix is a value that turns out to be useful in a few branches of Mathematics, it is especially key in finding the inverse of a matrix
Determinant of a 2 x 2 Matrix
Finding the determinant of a square matrix that is 2 × 2 in size is quite straightforward.
For a matrix \begin{bmatrix} a & b \\ c & d \end{bmatrix}, the determinant is obtained by ad − bc.
Examples
(1.1)
B = \begin{bmatrix} 3 & 4 \\ {\text{-}}1 & 5 \end{bmatrix} , det( B ) = (3 × 5) − (-1 × 4) = 19
(1.2)
C = \begin{bmatrix} 0 & 5 \\ 2 & 7 \end{bmatrix} , det( C ) = (0 × 7) − (2 × 5) = –10
Determinant of a Square Matrix, 3 x 3
There are a few ways one can find the determinant of a 3 × 3 matrix.
We’ll focus on the method referred to as ‘expansion using minors and cofactors’ here.
Sometimes just referred to as expansion using minors.
Using this method with a (3 × 3) matrix involves breaking the matrix down into smaller (2 × 2) matrices and using them in a specific way.
Expansion using Minors and Cofactors Process
Minors:
If we have a standard 3 × 3 matrix:A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}
We’ll initially focus on making use of the element a_{11}.
If we erase the rest of the row and column elements in which a_{11} sits, we are left with a smaller (2 × 2) matrix.
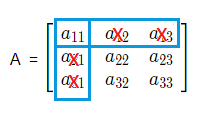
This new smaller (2 × 2) matrix is a ‘minor’ matrix, the notation for which is M_{11}.
M_{11} = \begin{bmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{bmatrix}
We can also do the same with elements a_{12} and a_{13} to get the follwoing.
M_{12} = \begin{bmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{bmatrix} M_{13} = \begin{bmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix}.
Each of these (2 × 2) minor matrices will have it’s own determinant.
Cofactors:
Now the ‘cofactor’ C of a matrix element a_{ij} is a number which is found by:\boldsymbol{C_{ij}} = \boldsymbol{({\text{-}}1)^{i+j}}det\boldsymbol{(M_{ij})}.
Thus the cofactor of a_{11} would be, \boldsymbol{C_{11}} = \boldsymbol{({\text{-}}1)^{1+1}}det\boldsymbol{(M_{11})}
Now we can look to put this all together.
If A is an n × n matrix. Then the determinant det(A) is given by:
det(A) = {\displaystyle\sum_{j=1}^n} a_{ij}({\text{-}}1)^{i+j}det(M_{ij})
So for our (3 × 3) matrix A, using the 1st row a entries, so i = 1, we have:
det(A) = {\displaystyle\sum_{j=1}^3} a_{1j}({\text{-}}1)^{i+j}det(M_{1j})
= {a_{11}({\text{-}}1)^{1+1}}det(M_{11}) + {a_{12}({\text{-}}1)^{1+2}}det(M_{12}) + {a_{13}({\text{-}}1)^{1+3}}det(M_{13})
= {a_{11}}det(M_{11}) − {a_{12}}det(M_{12}) + {a_{13}}det(M_{13})
The result we’ve ended up with above is the formula we can use to find the determinant of a square matrix of size 3 × 3.
This can be a lot to take in at first, but let’s see this formula in action with an example of a matrix involving numbers.
Example
(2.1)
Find the determinant of the matrix
G = \begin{bmatrix} 3 & 7 & 2 \\ 2 & {\text{-}}1 & 6 \\ 0 & 4 & 5 \end{bmatrix}.
Solution
We’ll again use the top row of elements to obtain our minor matrices.
a_{11} = 3 , a_{12} = 7 , a_{13} = 2
det(G) = {a_{11}}det(M_{11}) − {a_{12}}det(M_{12}) + {a_{13}}det(M_{13})
det(G) = (3 × det\begin{bmatrix} {\text{-}}1 & 6 \\ 4 & 5 \end{bmatrix}) − (7 × det\begin{bmatrix} 2 & 6 \\ 0 & 5 \end{bmatrix}) + (2 × det\begin{bmatrix} 2 & {\text{-}}1 \\ 0 & 4 \end{bmatrix})
= (3 × (-29)) − (7 × 10) + (2 × 8)
= –87 − 70 + 16 = –141
You can actually go along any row or column of a matrix performing the same method with minor matrices and get the same determinant value for the matrix.
Why not try it with this and other 3 x 3 matrices and see.
Determinants of Larger Matrices
While the approach shown on this page will work with any size of square matrix, once you get to matrices of size 4 x 4 and larger, the calculations can become quite time consuming.
For larger matrices we usually leave the work of finding the determinant to a computer or a matrix determinant calculator.
A good matrix determinant calculator can be found here at the symbolab website.