The rational roots test page showed how to find all the possible values of real roots or solutions that can a specific polynomial can have.
Descartes rule of signs is something that can tell us at most how many possible real roots/zeros we can expect a polynomial to have, along with what the nature of those roots will be, either positive or negative.
This page will demonstrate a selection of Descartes rule of signs examples in order to show how it can be used when dealing with polynomials.
Descartes Rules of Signs Intro
If we have a standard polynomial.
f(x) = \space a_nx^n \space + \space a_{n \space {\text{–}} \space 1}x^{n \space {\text{–}} \space 1} \space + ….. + \space a_{\tt{2}}x^{\tt{2}} \space \space + a_1x \space + \space a_0
What we look to do is count how many sign changes between + and − there are throughout the polynomial.
We do this for both f(x) and f({\text{-}}x).
Because for the sign changes between + and −.
The number of changes in f(x) tells us the number of possible positive real roots.
The number of changes in f({\text{-}}x) tells us the number of possible negative real roots.
Example
We can count how many sign changes there are in h(x) = x^3 + 4x^2 \space {\text{--}} \space 2x + 1.

But there may be less than 2 real positive roots, why?
Because there is a possibility of there being complex roots to the polynomial. Which always come in a conjugate pair.
If there are any complex roots, there will be an even number of them. 2 , 4 …….
Thus we count down by a size of 2 until we get to 1 or 0.
We can’t count down by 2 from 1, as we can’t have -1 roots/zeros.
So there are 0 or 2 real positive roots for h(x) = x^3 + 4x^2 \space {\text{–}} \space 2x + 1.
– Now for the case of h({\text{-}}x).
h({\text{-}}x) = ({\text{-}}x)^3 + 4({\text{-}}x)^2 \space {\text{–}} \space 2({\text{-}}x) + 1
Only the signs of terms with an odd power will change sign.
h({\text{-}}x) = {\text{-}}x^3 + 4x^2 + 2x + 1
We now have 1 sign change from − to +. h({\text{-}}x) = {\underbrace{{\text{-}}x^3}_{\text{{\color{red}1}}}} + 4x^2 + 2x + 1
As we can’t count down by 2 from 1.
There is definitely 1 negative real root to the original polynomial h(x)
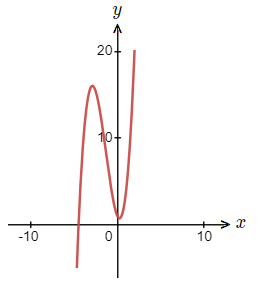
We can now look at the graph of h(x).
Where we see that there is just the 1 negative real root/zero, and in fact 0 positive real roots/zeros.
Descartes Rule of Signs Examples
(1.1)
Use Descartes rule of signs to establish the number possible real roots of f(x) = x^3 \space {\text{–}} \space 21x \space {\text{–}} \space 20.
Solution
f(x) = {\underbrace{x^3}_{\text{{\color{lightseagreen}1}}}} \space {\text{–}} \space 21x \space {\text{–}} \space 20
There is one positive real root for the polynomial.
f({\text{-}}x) = ({\text{-}}x)^3 \space {\text{–}} \space 21({\text{-}}x) \space {\text{–}} \space 20
= {\underbrace{{\text{-}}x^3}_{\text{{\color{red}1}}}} + {\underbrace{21x}_{\text{{\color{red}2}}}} \space {\text{–}} \space 20
There is possibly two negative real roots, or zero negative real roots.
Thus there is either three real roots to the polynomial, or one real root in total.
Note that the maximum number of possible real roots was 3.
Which happens to be the degree of the polynomial.
This is always the case when dealing with Descartes rule of signs examples.
So if you have a maximum number of possible roots that is larger or smaller after adding up the sign changes, then you know you have gone a bit wrong somewhere.
This is a handy fact to know as a way of checking.
(1.2)
With Descartes rule of signs to establish the number possible real roots of g(x) = x^5 \space {\text{–}} \space 6x^4 + 3x^3 + 36x^2 \space {\text{–}} \space 34x \space {\text{–}} \space 60.
Solution
g(x) = {\underbrace{x^5}_{\text{{\color{lightseagreen}1}}}} \space {\text{–}} \space {\underbrace{6x^4}_{\text{{\color{lightseagreen}2}}}} + 3x^3 + {\underbrace{36x^2}_{\text{{\color{lightseagreen}3}}}} \space {\text{–}} \space 34x \space {\text{–}} \space 60
There is three real positive roots, or just one positive real root.
g({\text{-}}x) = ({\text{-}}x)^5 \space {\text{–}} \space 6({\text{-}}x)^4 + 3({\text{-}}x)^3 + 36({\text{-}}x)^2 \space {\text{–}} \space 34({\text{-}}x) \space {\text{–}} \space 60
= {\text{-}}x^5 \space {\text{–}} \space 6x^4 \space {\text{–}} \space {\underbrace{3x^3}_{\text{{\color{red}1}}}} + {\underbrace{36x^2}_{\text{{\color{red}2}}}} \space {\text{–}} \space 34x \space {\text{–}} \space 60
There is possibly two negative real roots, or zero negative real roots.
Thus there is either five real roots, three real roots or one real root to the polynomial g(x).
Descartes Rule of Signs Summary
– Make sure the polynomial is in descending order of exponent value.– When switching to f({\text{-}}x), only the terms where the variable has an odd index have the sign changed.
– We may not end up with the exact number of real roots the polynomial has, unless the result is 0 or 1.
Due to the possible existence of complex roots.