The adding and subtracting fractions page showed some examples of how to add and subtract when dealing with sums involving fractions.
Sums such as \bf{\frac{3}{7}} + \bf{\frac{2}{7}} = \bf{\frac{3 \space + \space 2}{7}} = \bf{\frac{5}{7}},
and,
\bf{\frac{7}{9}} + \bf{\frac{5}{8}} = \boldsymbol{\frac{7 \space \times \space 8}{9 \space \times \space 8}} + \boldsymbol{\frac{5 \space \times \space 9}{8 \space \times \space 9}} = \bf{\frac{56}{72}} + \bf{\frac{40}{72}} = \bf{\frac{106}{72}} = \bf{\frac{53}{36}}.
This page will now show another method that can be used to add and subtract fractions effectively, a method referred to as the butterfly method for fractions.
It will become clear in the steps below why this method has this name.
Butterfly Method for Fractions Steps
To demonstrate how the butterfly method for fractions works,we’ll look at the fraction addition sum,
\bf{\frac{3}{4}} + \bf{\frac{5}{7}}.
Now the butterfly method is performed in 4 separate steps.
1)
Firstly write down the addition or subtraction fraction sum as usual.
Then draw two butterfly wings across both the diagonals, with an antenna rising out of the top of each wing.
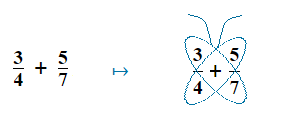
2)
Multiply the numbers in each separate wing of the butterfly together, and place the results under the antenna.
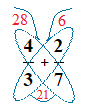
3 × 7 = 21 , 4 × 5 = 20
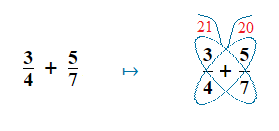
3)
Now we draw a loop underneath the wings to create the butterfly body.
Here we multiply the lower denominators together, and place the result in the newly created body.
4 × 7 = 28
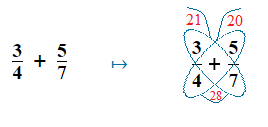
4)
The last step is to now add the numbers in the antenna together, then placing the result of this addition above the number in the body, to give us the answer to the original fractions addition sum.
\bf{\frac{21 \space + \space 20}{28}} = \bf{\frac{41}{28}}
So: \bf{\frac{3}{4}} + \bf{\frac{5}{7}} = \bf{\frac{41}{28}}.
This butterfly method for fractions also works with subtraction, which we’ll see in examples below.
Butterfly Method Examples
(1.1)
\bf{\frac{3}{2}} − \bf{\frac{5}{6}}
Solution
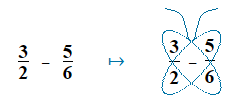
2 × 6 = 12
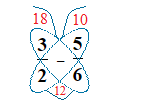
Now: \bf{\frac{18 \space {\text{--}} \space 10}{12}} = \bf{\frac{8}{12}} = \bf{\frac{2}{3}}
\bf{\frac{3}{2}} − \bf{\frac{5}{6}} = \bf{\frac{2}{3}}
(1.2)
\bf{\frac{4}{3}} + \bf{\frac{2}{7}}
Solution
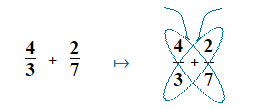
3 × 7 = 21
Now: \bf{\frac{28 \space + \space 6}{21}} = \bf{\frac{34}{21}}
\bf{\frac{4}{3}} + \bf{\frac{2}{7}} = \bf{\frac{34}{21}}
- Home ›
- Fractions and Decimals › Fractions Butterfly Method