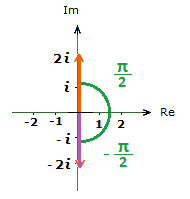
Sometimes referred to as the Complex Plane, an “Argand Diagram” is where we can plot and illustrate complex numbers.
Because complex numbers of the form a + bi, can be represented as a vector.
Argand Diagram Axis
On an Argand diagram, instead of an x and y axis, that we commonly see on a standard Cartesian Plane.
There is an Imaginary axis, and a Real axis.
Example
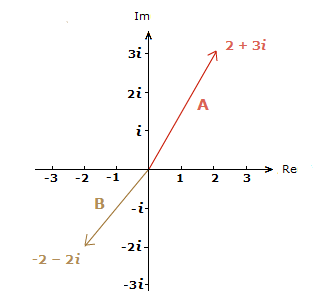
Consider the complex number A = 2 + 3i.
The REAL PART is 2, and the IMAGINARY PART is 3.
A can be drawn as a vector starting at the origin (0,0), and ending at the point (2,3).
Similarly, we can take the same approach with another complex number B = -2 − 2i.
Polar Form & Polar Coordinates,
Complex Number Modulus
A complex number can also be represented on the Argand diagram with what’s called Polar Coordinates.
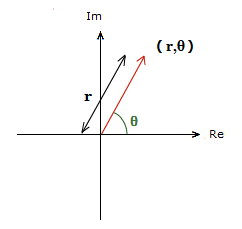
The vector position would now be represented by (r,θ).
These values come from the POLAR FORM of a complex number.
Which is z = r(cosθ + isinθ), as opposed to z = a + ib.
To further understand this, consider a similar diagram to the one above.
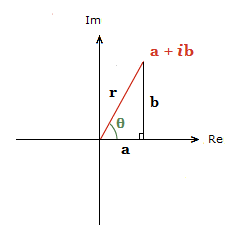
Here r is the modulus of z, and is the magnitude/size of the vector. Generally denoted |z|.
To establish r, we do the sum r = \bf{\sqrt{a^2 \space + \space b^2}}.
θ is the angle the vector makes with the positive direction of the Real axis. Usually in Radians, but can be in degrees also.
This is called the argument of z, denoted Arg(z).
From the triangle diagram above, using the Trig Ratios concerning θ.
cosθ = \bf{\frac{a}{r}} sinθ = \bf{\frac{b}{r}}
Multiplying both sides of both terms by r gives.
rcosθ = a rsinθ = b
So a complex number of the form z = a + ib, can become:
z = rcosθ + irsinθ = r(cosθ + isinθ).
This form can also be shortened to r cis θ.
But they represent the same thing.
For example, 4(cos(\bf{\frac{\pi}{2}}) + isin(\bf{\frac{\pi}{2}})) = 4 cis \bf{\frac{\pi}{2}}.
Polar Form Argument
As we’ve seen above, if we want to convert a complex number from the form z = a + ib into the form z = r(cosθ + isinθ).
Working out the modulus r is straightforward.
[ r = \bf{\sqrt{a^2 \space + \space b^2}} ]
However, a little more care needs to be taken for the Argument θ.
If we refer to the Trigonometric Ratios for θ again. It’s the case that tanθ = \bf{\frac{b}{a}}.
At first some people can sometimes assume that to obtain θ, we can always just do
tan-1(\bf{\frac{b}{a}}) = θ.
But attention needs to be paid to which quadrant of the diagram the vector is actually in.
It’s the case that tan-1(\bf{\frac{b}{a}}) will produce a value between –\bf{\frac{\pi}{2}} and \bf{\frac{\pi}{2}}, or –90° and 90° in degrees.
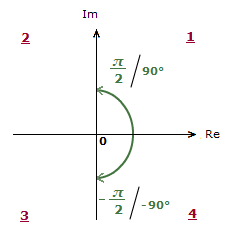
Now this is fine for Quadrants 1 and 4.
But sometimes, a little extra step is needed to obtain an accurate Polar Form for quadrants 3 and 4. Depending on the values of a and b.
Let’s look at the variations of a complex number in the form z = a + ib.
Case where a > 0:
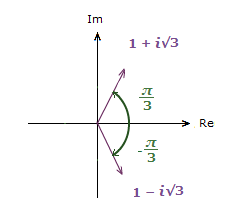
1) 1 + i√3 2) 1 − i√3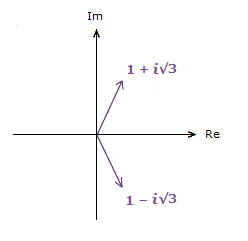
1) θ = tan-1(\bf{\frac{\sqrt{3}}{1}}) = \bf{\frac{\pi}{3}} 2) θ = tan-1(\bf{\frac{{\text{-}}\sqrt{3}}{1}}) = –\bf{\frac{\pi}{3}}
Case 1) is fine, that’s in the 1st quadrant.
Case 2) is also fine. The value of θ is in the 4th quadrant where the vector is.
Case where a < 0:
3) -1 + i√3 4) -1 − i√3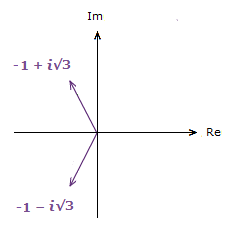
3) θ = tan-1(\bf{\frac{\sqrt{3}}{{\text{-}}1}}) = –\bf{\frac{\pi}{3}} 4) θ = tan-1(\bf{\frac{{\text{-}}\sqrt{3}}{{\text{-}}1}}) = \bf{\frac{\pi}{3}}
Now here, with a < 0, we’re really to the left of the Imaginary axis, so a little extra step is required.
For 3), add to π. => π + -(\bf{\frac{\pi}{3}}) = \bf{\frac{2\pi}{3}}
For 4), add to –π. => –π + \bf{\frac{\pi}{3}} = –\bf{\frac{2\pi}{3}}
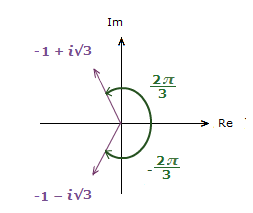
So putting vectors 1), 2), 3) and 4) into POLAR FORM.
The modulus r is the same value each time, 2. As each vector is the same size/magnitude.
But the angle θ is different.
1 + i√3 => z = 2(cos(\bf{\frac{\pi}{3}}) + isin(\bf{\frac{\pi}{3}}))
1 − i√3 => z = 2(cos(-\bf{\frac{\pi}{3}}) + isin(-\bf{\frac{\pi}{3}}))
–1 + i√3 => z = 2(cos(\bf{\frac{2\pi}{3}}) + isin(\bf{\frac{2\pi}{3}}))
–1 − i√3 => z = 2(cos(-\bf{\frac{2\pi}{3}}) + isin(-\bf{\frac{2\pi}{3}}))
Summary
A complex number can be in Cartesian Form, and Polar Form.
CARTESIAN FORM: z = a + bi
POLAR FORM: z = r(cosθ + isinθ)
When converting from Cartesian to Polar Form.
Make sure to pay attention to the a and b values.
– If a > 0, b > 0, θ = tan-1(\bf{\frac{b}{a}})
– If a > 0, b < 0, θ = tan-1(\bf{\frac{b}{a}})
– If a < 0, b > 0, θ = π + tan-1(\bf{\frac{b}{a}})
– If a < 0, b < 0, θ = –π + tan-1(\bf{\frac{b}{a}})
There is also the case where
a = 0, b < 0 or a = 0, b > 0.
When this happens, the vector on the Argand diagram will be either straight up, or straight down on the Imaginary axis.
So:
– If a = 0, b > 0, θ = \bf{\frac{\pi}{2}}
– If a = 0, b < 0, θ = –\bf{\frac{\pi}{2}}