The simplest method to work out the area of a triangle is using the following formula.
Area = \bf{\frac{1}{2}} × BASE × HEIGHT
Provided that we know the values of both the BASE and the HEIGHT of a triangle.
Triangles in a Rectangle/Square
The formula arises because a rectangle or square is made up of 2 right angle triangles.
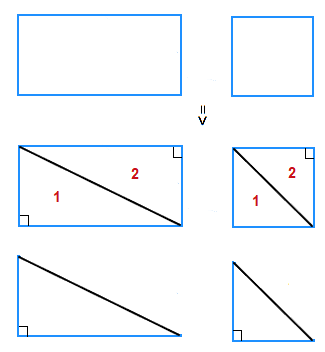
With the area of a rectangle/square being, BASE × HEIGHT.
This leads to the area of a triangle being, \frac{1}{2} × BASE × HEIGHT.
This holds for other triangles too, and not just right angle triangles.
For example, with the following 2 triangles.
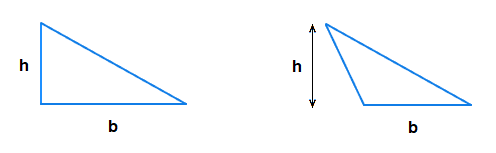
Despite the difference in how they appear, the area of both triangles can be obtained by using the same formula shown above.
Area of a Triangle Examples
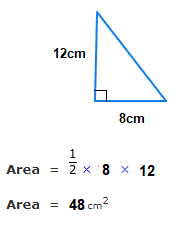
(1.1)
(1.2)
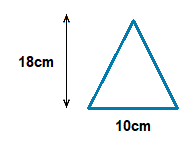
Area = \bf{\frac{1}{2}} × 10 × 18 = \bf{\frac{1}{2}} × 180
Area = 90cm2
(1.3)
The following triangle has an area of size 20cm2.
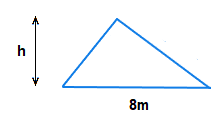
What is the the height of the triangle?
Solution
Area = \bf{\frac{1}{2}} × BASE × HEIGHT
20 = \bf{\frac{1}{2}} × 8 × HEIGHT
20 = 4 × HEIGHT
\bf{\frac{20}{4}} = HEIGHT = 5
The height of the triangle is 5m.
Area of a Triangle Examples, Heron’s Formula
Another way of dealing with area of a triangle examples is by using what is known as “Heron’s Formula”.
If we have a standard triangle such as the one pictured below.
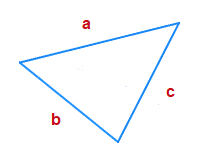
Then a value for the area can be obtained with the following approach.
Firstly, we look to work out half of the triangle perimeter, denoted s.
s = \tt{\frac{a \space + \space b \space + \space c}{2}}
Then, we use this value s in a further formula to work out the area of the triangle.
Area = \tt{\sqrt{s(s-a)(s-b)(s-c)}}
Example
(2.1)
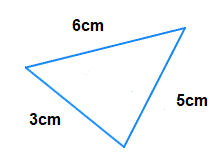
s = \bf{\frac{6 \space + \space 5 \space + \space 3}{2}} = \bf{\frac{14}{2}} = 7
Area = \bf{\sqrt{7(7-6)(7-5)(7-3)}}
= \bf{\sqrt{7 \times 1 \times 2 \times 4}} = √56 = 7.48cm2