An Octagon is a shape that has exactly 8 sides.
With a regular Octagon having 8 sides that are of equal length.
Area of a Regular Octagon Formula
The area of a regular Octagon can be found with by a standard formula, which we can derive and establish here.
Triangles in a Regular Octagon
As well as having 8 sides that are of equal length.
A regular Octagon also has 8 interior isosceles triangles that are of equal size.
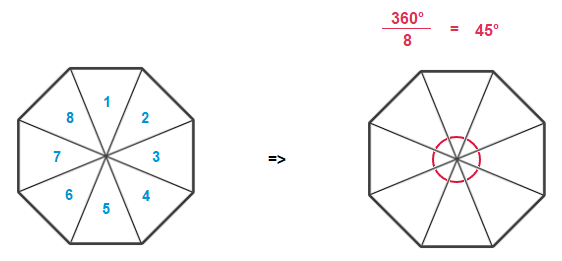
We can focus on one of these triangles, and observe that it can be halved into a smaller right angle triangle.
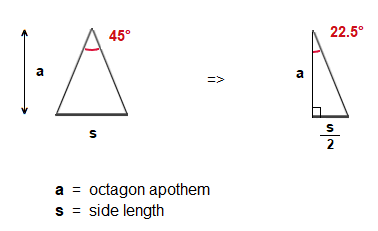
Using the Triangles to find Regular Octagon Area
Firstly looking at the smaller right angle triangle.
We look at the angle 22.5°.
The tan ratio is the opposite side over the adjacent side.
So we have.
tan( 22.5° ) = \frac{\frac{{\scriptsize{s}}}{2}}{\space {\tt{a}} \space}
Which can be written as. tan( 22.5° ) = \frac{s}{\space 2{\tt{a}} \space}
From here we can do a bit more work to obtain an expression for a.
\frac{1}{{\tt{tan}}(22.5)} = \frac{2{\tt{a}}}{\space s \space} ( × s )
\frac{s}{{\tt{tan}}(22.5)} = 2{\tt{a}} ( ÷ 2 )
\frac{s}{2{\tt{tan}}(22.5)} = {\tt{a}}
Using expression for “a” to obtain Area Formula
It’s the case that tan( 22.5 ) can be written as \sqrt2 \space {\text{--}} \space 1.
Which gives us. \frac{s}{2(\sqrt2 \space {\text{--}} \space 1)} = {\tt{a}}
The area of one of the 8 smaller inside triangles is. \frac{1}{2} × BASE × HEIGHT
So the total Octagon area is all the inside triangles together. \frac{1}{2} × BASE × HEIGHT × 8
Area = \frac{1}{2} × s × \frac{{\small{s}}}{2(\sqrt2 \space {\text{--}} \space 1)} × 8
= \frac{8s^2}{4(\sqrt2 \space {\text{--}} \space 1)} = \frac{2s^2}{\space \sqrt2 \space {\text{--}} \space 1 \space}
From here we can make things a bit neater.
\frac{2s^2}{\space \sqrt2 \space {\text{--}} \space 1 \space} × \frac{\sqrt2 + 1}{\space \sqrt2 + 1 \space} = \frac{2s^2 \sqrt2 \space\space + \space\space 2s^2}{\space 2 \space {\text{--}} \space 1 \space}
= s^2(2 \sqrt2 \space + \space 2)
Thus to work out a value for the area of a regular Octagon, as long as we know a side length s.
We can do the sum, s^2(2 \sqrt2 \space + \space 2).
Area of a Regular Octagon Examples
(1.1)
What is the area of the following regular Octagon to 2 decimal places?
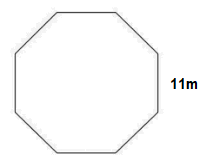
Solution
Area = ( 11 )^2 (2\sqrt2 + 2)
= 121 \times (2\sqrt2 + 2) = 584.24
The area of the regular Octagon is 584.24m2.
(1.2)
A regular Octagon has an area of 340cm2.
Roughly what size is each side length s.
Solution
340 \space\space = \space\space s^2(2 \sqrt2 \space + \space 2)
{\Large{\frac{340}{2 \sqrt2 \space + \space 2}}} \space\space = \space\space s^2
70.42 \space\space = \space\space s^2
\sqrt{70.42} \space\space = \space\space s \space\space = \space\space 8.39
Each side of the regular Octagon is roughly 8.39cm.