A Heptagon in Math is a shape that has 7 sides in total.
With a regular Heptagon having 7 sides that are all of equal length.
Here we will look at how we can establish the area of a regular Heptagon.
Area of a regular Heptagon Formula
We can look at the shape of a standard regular Heptagon.
With this Heptagon, we can draw straight lines from the central point of the Heptagon, to each corner.
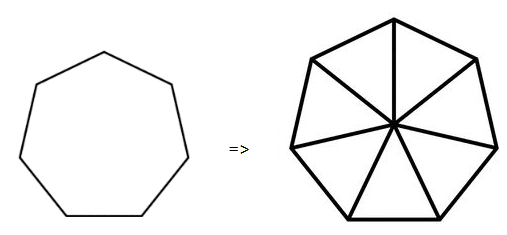
What these straight lines do, is create 7 identical isosceles triangles inside the Heptagon.
If we recall that in a full circle there is 360°.
The inner angle of each triangle will be of size 360° divided by 7.
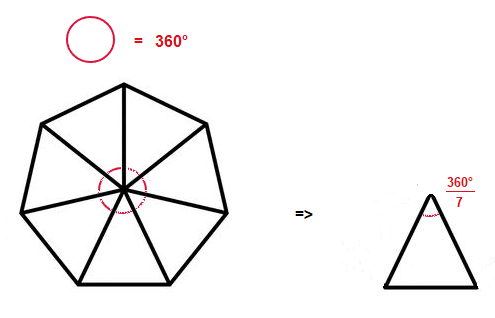
From here, we can look further at one of the 7 interior triangles, and what happens when we split the triangle in half.
Triangles in a Heptagon
The area of one of the 7 interior triangles, multiplied by 7 gives the whole regular Heptagon area.
Firstly if we focus on the right angle triangle that is one half of the larger interior isosceles triangle.
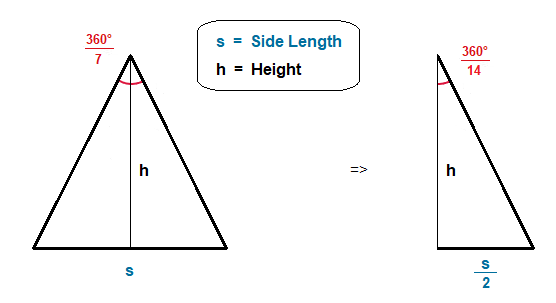
This smaller right angle triangle can help give us an expression for the height h.
We can use Pythagoras, by recalling that the tan ratio is the opposite side over the adjacent side.
For angle \frac{360\degree}{14}. The opposite side is \frac{\tt{s}}{2}, and the adjacent side is h.
tan(\frac{360\degree}{14}) = \frac{\frac{s}{2}}{\space {\tt{h}}\space} => tan(\frac{360\degree}{14}) = \frac{s}{2{\tt{h}}}
( Writing 1 over the left side will flip the fraction on the right.
The ratio \frac{1}{\tt{tan}} can be written as cot. )
\frac{1}{{\tt{tan}}(\frac{360\degree}{14})} = \frac{2{\tt{h}}}{s} => cot(\frac{360\degree}{14}) = \frac{2{\tt{h}}}{s}
( We can multiply both sides by \frac{\tt{s}}{2}. )
\frac{{\tt{s \space cot}} (\frac{360\degree}{14})}{2} = h
Putting this together to find
Regular Heptagon Area:
So now we have an expression for the height h of one of the interior triangles.
The area of a triangle can be obtained by doing a half multiplied by the base and the height.
Seven of these triangles make up the whole area of a regular Heptagon.
So to find the area of a regular Heptagon we can do as follows.
Heptagon Area = 7 × \frac{1}{2} × s × h
= 7 × \frac{1}{2} × s × \frac{{\tt{s \space cot}} (\frac{360\degree}{14})}{2}
= \frac{7}{2} × \frac{{\tt{s^2 \space cot}} (\frac{360\degree}{14})}{2} = \frac{7{\tt{s^2 \space cot}} (\frac{360\degree}{14})}{4}
( From this result we can separate the s2. )
Heptagon Area = s2 × \frac{7{\tt{cot}} (\frac{360\degree}{14})}{4}
\frac{7{\tt{cot}} (\frac{360\degree}{14})}{4} actually has a numerical value which is 3.634, to 3 decimal places.
So provided we know the side length of a regular Heptagon, s
Heptagon Area ≈ s2 × 3.634
Area of a Regular Heptagon Examples
(1.1)
What is the area of the following Heptagon?
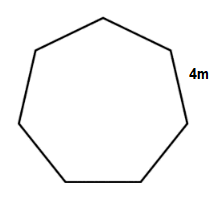
Solution
Area ≈ 42 × 3.634
Area ≈ 58.14m2
(1.2)
Roughly what is the side length of a regular Heptagon with an area of 426cm2.
Solution
426 ≈ 3.634 × s2
\bf{\frac{{\tt{426}}}{{\tt{3.634}}}} ≈ s2 => 117.23 ≈ s2
\sqrt{\tt{\bf{117.23}}} ≈ s => 10.83 ≈ s
A regular Heptagon with an area of 426cm2 has a side length of roughly 10.83cm.